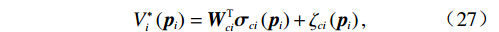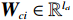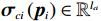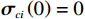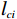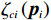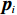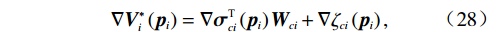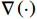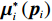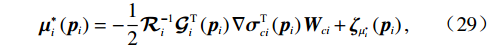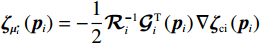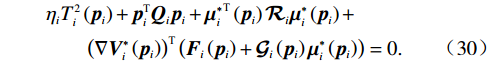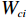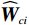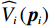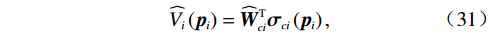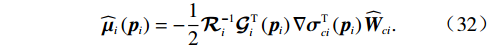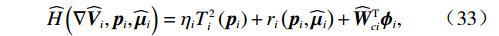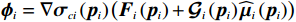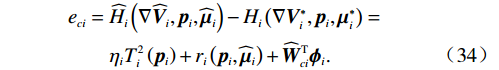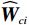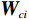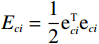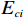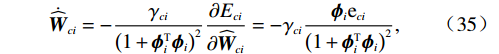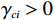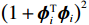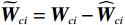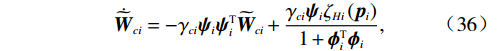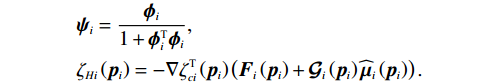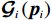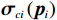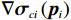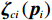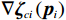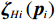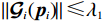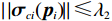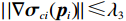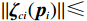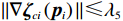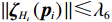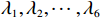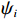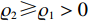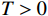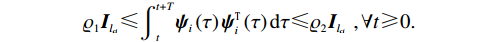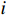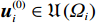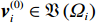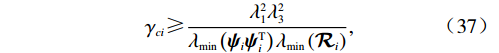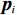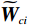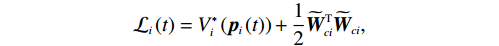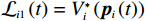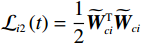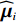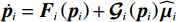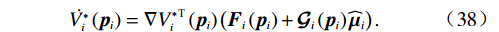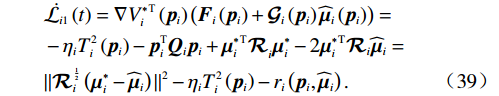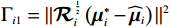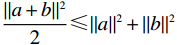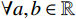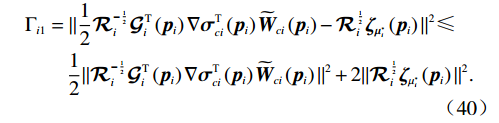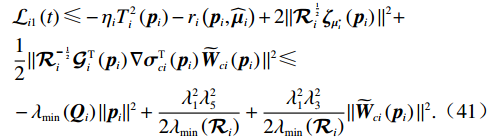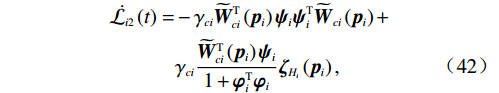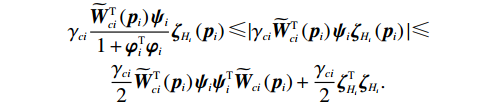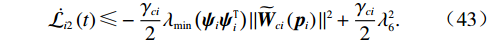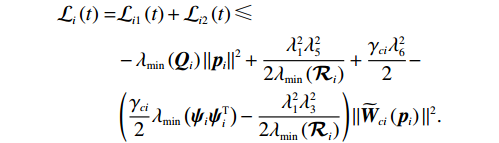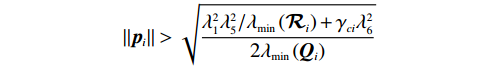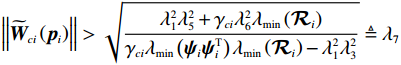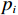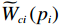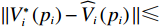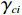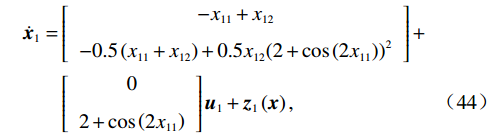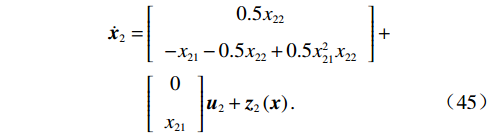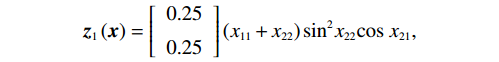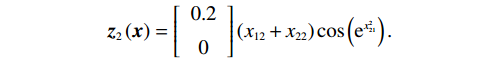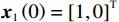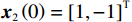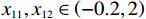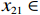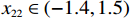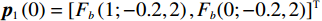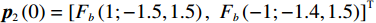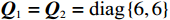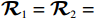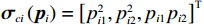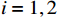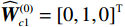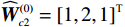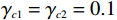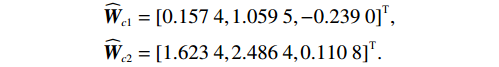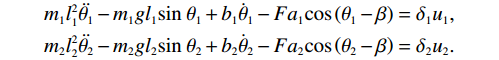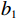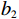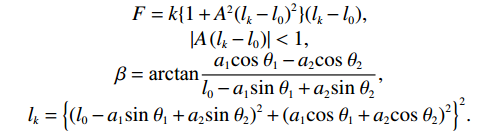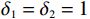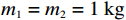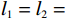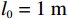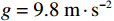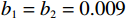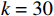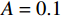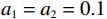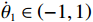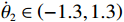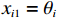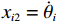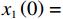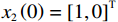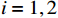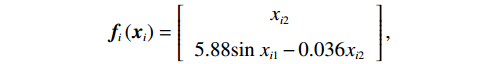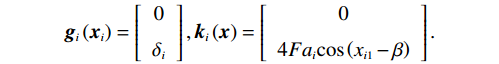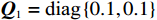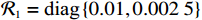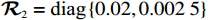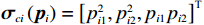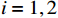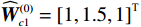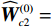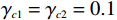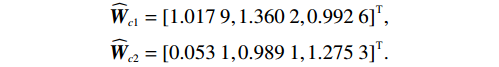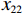Decentralized stabilization of state constrained interconnected nonlinear systems based on adaptive dynamic programming
-
摘要: 针对一类含有常数型状态约束的互联非线性系统,提出一种基于自适应动态规划(adaptive dynamic programming,ADP)的分散镇定方法.引入边界函数对原系统进行坐标变换,将状态约束系统转化为无约束系统.对转化后的系统构造独立子系统和改进的代价函数,将鲁棒分散镇定问题转化为最优调节问题.构建局部评判神经网络并采用策略迭代算法求解哈密顿-雅可比-贝尔曼(Hamilton-Jacobi-Bellman,HJB)方程,进而得到近似最优镇定律.通过李雅普诺夫稳定性理论证明了本文所提方法可使闭环互联系统和局部评判神经网络估计误差动态最终一致有界.数值仿真结果验证了所提出分散镇定方法的有效性.Abstract: A decentralized stabilization method based on adaptive dynamic programming (ADP) is proposed for a class of interconnected nonlinear systems with constant-value state constraints. A barrier function is introduced so that the original system is converted into an unconstrained system by coordinate transformation. Auxiliary subsystems and improved cost functions enabled transformation of robust decentralized stabilization problem into an optimal regulation problem. The Hamilton-Jacobi-Bellman (HJB) equation is solved by policy iteration after constructing a local critic neural network for each auxiliary subsystem so that an approximate optimal stabilization control law is obtained. According to the Lyapunov stability theory, the proposed method can drive estimation errors of closed-loop interconnected system and local critic neural networks to be ultimately uniformly bounded dynamically. Numerical simulations validate the effectiveness of proposed decentralized stabilization method.
-
0 引言
系统科学是一门研究系统行为、结构、环境和功能之间普适关系,进而分析与设计系统演化与调控规律的交叉性学科.控制论作为系统科学的重要分支,旨在研究如何设计和优化控制策略,以使系统在不确定性和变化的环境中能够达到满意的稳定性、准确性、快速性等预设的性能要求[1].在现实世界中,许多系统是由多个动态互联的子系统组成的,此类系统广泛存在于工程、电力、交通、经济、社会等领域[2].由于其规模庞大,且不同子系统的状态之间存在关联,难以对整个互联系统设计集中控制器.因此,针对各个子系统分别设计控制律,构成一组控制器控制整个大规模系统[3−4]的分散控制方式得到了广泛应用.
随着系统规模的不断扩大,人们对于这类系统的控制精度、响应速度、优化性能等指标均有更高的要求.PID控制等经典控制方法难以满足这类系统稳定性和性能指标最优性的要求.自适应动态规划(adaptive dynamic programming, ADP)作为一种基于动态规划、强化学习、神经网络等方法的智能控制理论,能够处理系统的非线性特性和不确定性,因此对解决非线性系统的最优控制问题非常适用[5].目前,ADP理论与方法已广泛应用于系统的状态调节、输出调节、轨迹跟踪、容错控制等问题[5−9].在实际应用方面,ADP已成功用于解决电网控制[10]、电机调速[11]、地铁调度[12]等问题.此外,ADP在解决含约束系统的控制问题上也做了一些有益尝试.
由于系统固有组件自身特性的限制和系统运行安全的要求,系统的运行状态以及执行器输出通常会受到约束[13−14],这增大了控制系统设计的难度.模型预测控制是一种解决含状态约束系统控制问题的有效方法[15],但这种方法具有很高的计算复杂度.边界李雅普诺夫函数法也可用于处理系统的状态约束[16],但这种方法通常对非线性系统结构有特定要求,如必须是严格反馈形式的非线性系统.在最优控制理论中,松弛函数法可处理控制过程的约束条件,因此也能够用于解决状态约束系统的控制问题.Fan等[17]引入松弛函数,将含状态约束的非线性系统控制问题转化为无约束非线性系统控制问题,并在此基础上实现原系统的容错控制;Xie等[18]引入边界李雅普诺夫函数,研究了具有参数不确定性、外部干扰和执行器故障的状态约束线性系统的容错控制问题;Yang等[19]构造了一种用于处理全状态约束的边界函数,实现了在含有输入约束和全状态约束的情况下对非线性系统的鲁棒控制;Song等[20]运用边界函数处理状态约束,并引入事件触发机制,实现了同时包含输入与状态约束的非线性系统的
$ H_\infty $ 控制.然而,以上方法考虑的均为单一系统,未考虑互联系统中各子系统状态之间存在的耦合性.本文引入边界函数,通过坐标变换将含有常数型状态约束的互联非线性系统镇定问题转化为无约束互联非线性系统的镇定问题,对变换后的系统构建不含耦合项的独立子系统.针对各个独立子系统分别设计含辅助控制律的值函数和哈密顿-雅可比-贝尔曼(Hamilton-Jacobi-Bellman, HJB)方程,并通过局部评判神经网络求解得到近似最优镇定律.本文采用的2个仿真实例将该方法与未处理状态约束的ADP镇定方法进行了对比,验证了其有效性.
1 问题描述与系统变换
含
$N $ 个子系统的互联非线性系统为$$ {\dot{{\boldsymbol{x}}}}_{i}={{\boldsymbol{f}}}_{i}\left({{\boldsymbol{x}}}_{i}\left(t\right.\right))+{{\boldsymbol{g}}}_{i}\left({{\boldsymbol{x}}}_{i}\left(t\right)\right){{\boldsymbol{u}}}_{i}\left(t\right)+{{\boldsymbol{z}}}_{i}\left(\boldsymbol {x}\left(t\right)\right), $$ (1) 式中:
$ i={1,2},\cdots ,N $ ;$ {{\boldsymbol{x}}}_{i}\left(t\right)\in {\mathbb{R}}^{{n}_{i}} $ ;$ {{\boldsymbol{u}}}_{i}\left(t\right)\in {\mathbb{R}}^{{m}_{i}} $ 分别是第$ i $ 个子系统的状态和控制输入,第$ i $ 个子系统的第$ j $ 维状态$ {x}_{ij} $ 满足$ {c}_{ij} < {x}_{ij} < {d}_{ij} $ ($ {c}_{ij} < 0 $ ,$ {d}_{ij} > 0 $ ,$ j={1,2},\cdots ,{n}_{i} $ );$ {c}_{ij} $ 、$ {d}_{ij} $ 分别为$ {x}_{ij} $ 的下界和上界约束.$ {{{\boldsymbol{f}}}}_{i}\left({\boldsymbol{x}}_{i}\right)\in {\mathbb{R}}^{{n}_{i}} $ 、$ {{{\boldsymbol {g}}}}_{i}\left({\boldsymbol {x}}_{i}\right)\in {\mathbb{R}}^{{n}_{i}\times {m}_{i}} $ 均为光滑的非线性函数,分别表示系统动态和控制输入矩阵,$ {{\boldsymbol{z}}}_{i}\left(x\right)\in {\mathbb{R}}^{{n}_{i}} $ 是第$ i $ 个子系统与其他子系统之间的耦合项.受文献[19−20]启发,本文采用边界函数(2),将原互联系统的约束状态
$ {x}_{ij} $ 转化为不含约束的状态$ p_{ij} $ ,如$$ {p}_{ij}={F}_{b}\left({x}_{ij};{c}_{ij},{d}_{ij}\right)=\mathrm{ln}\left(\frac{{d}_{ij}}{{c}_{ij}}\frac{{c}_{ij}-{x}_{ij}}{{d}_{ij}-{x}_{ij}}\right), $$ (2) 其中
$ \forall {x}_{ij}\in \left({c}_{ij},{d}_{ij}\right) $ ,则式(2)的反函数为$$ {x}_{ij}={F}_{b}^{-1}\left({p}_{ij};{c}_{ij},{d}_{ij}\right)=\frac{{c}_{ij}{d}_{ij}\left({e}^{{p}_{ij}}-1\right)}{{c}_{ij}{e}^{{p}_{ij}}-{d}_{ij}}, $$ (3) 其中
$ \forall {p}_{ij}\in \mathbb{R} $ .将$ {F}_{b}^{-1}\left({p}_{ij};{c}_{ij},{d}_{ij}\right) $ 简记为$ {F}_{b}^{-1}\left({p}_{ij}\right) $ ,将$ {{\boldsymbol{f}}}_{i}\left({\boldsymbol {x}}_{i}\right) $ 、$ {{\boldsymbol{g}}}_{i}\left({\boldsymbol {x}}_{i}\right) $ 、$ {{\boldsymbol{z}}}_{i}\left(\boldsymbol {x}\right) $ 的第$ j $ 行元素分别记为$ {f}_{ij}\left({\boldsymbol {x}}_{i}\right) $ 、$ {g}_{ij}\left({\boldsymbol {x}}_{i}\right) $ 、$ {z}_{ij}\left(\boldsymbol {x}\right) $ .通过式(3)将原系统(1)化为$$ \left[\begin{array}{c}\dot{F}_{b}^{-1}\left({p}_{i1}\right)\\ \vdots\\ \dot{F}_{b}^{-1}\left({p}_{i{n}_{i}}\right)\end{array}\right]={{\boldsymbol{F}}}_{si}\left({{\boldsymbol{p}}}_{i}\right)+{{\boldsymbol{G}}}_{si}\left({{\boldsymbol{p}}}_{i}\right){{\boldsymbol{u}}}_{i}+{{\boldsymbol{Z}}}_{si}\left({\boldsymbol{p}}\right), $$ (4) 式中,p为式(1)中x(t)经变换后所得的状态.
$$ {{\boldsymbol{F}}}_{si}\left({{\boldsymbol{p}}}_{i}\right)=\left[\begin{array}{c}{f}_{i1}\left({\left[{F}_{b}^{-1}\left({p}_{i1}\right),\cdots ,{F}_{b}^{-1}\left({p}_{i{n}_{i}}\right)\right]}^{\mathrm{T}}\right)\\ \vdots\\ {f}_{i{n}_{i}}\left({\left[{F}_{b}^{-1}\left({p}_{i1}\right),\cdots ,{F}_{b}^{-1}\left({p}_{i{n}_{i}}\right)\right]}^{\mathrm{T}}\right)\end{array}\right], $$ $$ {{\boldsymbol{G}}}_{si}\left({{\boldsymbol{p}}}_{i}\right)=\left[\begin{array}{c}{g}_{i1}\left({\left[{F}_{b}^{-1}\left({p}_{i1}\right),\cdots ,{F}_{b}^{-1}\left({p}_{i{n}_{i}}\right)\right]}^{\mathrm{T}}\right)\\ \vdots\\ {g}_{i{n}_{i}}\left({\left[{F}_{b}^{-1}\left({p}_{i1}\right),\cdots ,{F}_{b}^{-1}\left({p}_{i{n}_{i}}\right)\right]}^{\mathrm{T}}\right)\end{array}\right], $$ $$ {{\boldsymbol{Z}}}_{si}\left({\boldsymbol{p}}\right)=\left[\begin{array}{c}{z}_{i1}\left({\left[{F}_{b}^{-1}\left({p}_{i1}\right),\cdots ,{F}_{b}^{-1}\left({p}_{N{n}_{N}}\right)\right]}^{\mathrm{T}}\right)\\ \vdots\\ {z}_{i{n}_{i}}\left({\left[{F}_{b}^{-1}\left({p}_{i1}\right),\cdots ,{F}_{b}^{-1}\left({p}_{N{n}_{N}}\right)\right]}^{\mathrm{T}}\right)\end{array}\right]. $$ 将式(3)对
$ {p}_{ij} $ 求偏导可得$$\frac{{\rm{d}}{F}_{b}^{-1}\left({p}_{ij};{c}_{ij},{d}_{ij}\right)}{{\rm{d}}{p}_{ij}}=\frac{{d}_{ij}{c}_{ij}^{2}-{c}_{ij}{d}_{ij}^{2}}{{c}_{ij}^{2}{e}^{{p}_{ij}}+{d}_{ij}^{2}{e}^{-{p}_{ij}}-2{c}_{ij}{d}_{ij}}. $$ (5) 记
$ {F}_{bpij}=\dfrac{{c}_{ij}^{2}{e}^{{p}_{ij}}+{d}_{ij}^{2}{e}^{-{p}_{ij}}-2{c}_{ij}{d}_{ij}}{{d}_{ij}{c}_{ij}^{2}-{c}_{ij}{d}_{ij}^{2}} $ .因此,经坐标变换后的系统状态可表示为$$ \begin{split} {\dot{p}}_{ij}=\;&\frac{{\dot{x}}_{ij}}{\dfrac{{\rm{d}}{F}_{b}^{-1}\left({p}_{ij};{c}_{ij},{d}_{ij}\right)}{{\rm{d}}{p}_{ij}}}={F}_{bpij}{\dot{x}}_{ij}={F}_{bpij}\cdot{F}_{b}^{-1}\left({p}_{ij}\right) =\\ &{f}_{ij}\left({{\boldsymbol{p}}}_{i}\right)+{g}_{ij}\left({{\boldsymbol{p}}}_{i}\right){\boldsymbol{u}}_{i}\left(t\right)+{z}_{ij}\left(\boldsymbol {p}\right). \end{split} $$ (6) 通过式(6)可将式(4)进一步化为
$$ \dot{{{\boldsymbol{p}}}_{i}}\left(t\right)={{\boldsymbol{F}}}_{i}\left({{\boldsymbol{p}}}_{i}\left(t\right)\right)+{{\boldsymbol{G}}}_{i}\left({{\boldsymbol{p}}}_{i}\left(t\right)\right){{\boldsymbol{u}}}_{i}\left(t\right)+{{\boldsymbol{Z}}}_{i}\left({\boldsymbol{p}}\right),$$ (7) 式中:
$$ {{\boldsymbol{p}}}_{i}={\left[{p}_{i1},{p}_{i2},\cdots ,{p}_{i{n}_{i}}\right]}^{\text{T}}, $$ $$ {{\boldsymbol{F}}}_{i}\left({{\boldsymbol{p}}}_{i}\right)=\text{diag}\left\{{F}_{bpi1},\cdots ,{F}_{bpi{n}_{i}}\right\}\cdot{{\boldsymbol{F}}}_{si}\left({{\boldsymbol{p}}}_{i}\right), $$ $$ {{\boldsymbol{G}}}_{i}\left({{\boldsymbol{p}}}_{i}\right)=\text{diag}\left\{{F}_{bpi1},\cdots ,{F}_{bpi{n}_{i}}\right\}\cdot{{\boldsymbol{G}}}_{si}\left({{\boldsymbol{p}}}_{i}\right), $$ $$ {{\boldsymbol{Z}}}_{i}\left({\boldsymbol{p}}\right)=\text{diag}\left\{{F}_{bpi1},\cdots ,{F}_{bpi{n}_{i}}\right\}\cdot{{\boldsymbol{Z}}}_{si}\left({\boldsymbol{p}}\right). $$ 为便于后续进行分散镇定律设计和稳定性分析,对变换后的互联系统(7),定义如下假设.
假设1
$ {{\boldsymbol{F}}}_{i}\left({{\boldsymbol{p}}}_{i}\right) $ 和$ {{\boldsymbol{G}}}_{i}\left({{\boldsymbol{p}}}_{i}\right) $ 是Lipschitz连续的,且$ {{\boldsymbol{p}}}_{i}=0 $ 为系统(7)的平衡点.假设2 耦合项
$ {{\boldsymbol{Z}}}_{i}\left({\boldsymbol{p}}\right) $ 满足非匹配条件$$ {{\boldsymbol{Z}}}_{i}\left({\boldsymbol{p}}\right)={{\boldsymbol{K}}}_{i}\left({{\boldsymbol{p}}}_{i}\right){{\boldsymbol{D}}}_{i}\left({\boldsymbol{p}}\right)\left({{\boldsymbol{K}}}_{i}\left({{\boldsymbol{p}}}_{i}\right)\ne {{\boldsymbol{G}}}_{i}\left({{\boldsymbol{p}}}_{i}\right)\right), $$ (8) 式中:
$ {{\boldsymbol{K}}}_{i}\left({{\boldsymbol{p}}}_{i}\right)\in {\mathbb{R}}^{{n}_{i}\times {w}_{i}} $ 是已知的光滑函数;$ {{\boldsymbol{D}}}_{i}\left({\boldsymbol{p}}\right)\in {\mathbb{R}}^{{w}_{i}} $ 为不确定项,其上界满足$$ |{|{\boldsymbol{D}}}_{i}\left({\boldsymbol{p}}\right)\|\leqslant {a}_{i}\sum _{m=1}^{N}{\alpha }_{m}\left(|{|\boldsymbol {p}}_{m}\|\right),m={1,2},\cdots ,N, $$ (9) 式中:
$ {a}_{i}\geqslant 0\left(i={1,2},\cdots ,N\right) $ 为非负常数;$ {\mathrm{\alpha }}_{m}\left(\cdot\right) $ 为半正定函数,且$ {\mathrm{\alpha }}_{m}\left(0\right)=0 $ ,$ m={1,2},\cdots ,N $ .假设3 存在函数
$ {\mathrm{\beta }}_{l}\left(\cdot\right) $ ,$ l={1,2},\cdots ,N$ .使$$ \|{{\boldsymbol{G}}}_{i}^+\left({{\boldsymbol{p}}}_{i}\right){{\boldsymbol{Z}}}_{i}\left({\boldsymbol{p}}\right)\|\leqslant \sum _{l=1}^{N}{e}_{il}{{\beta }}_{l}\left(\|{\boldsymbol {p}}_{l}||\right), $$ (10) 式中:
$ {{\boldsymbol{G}}}_{i}^{+}\left({{{{\boldsymbol{p}}}}}_{i}\right) $ 为$ {{\boldsymbol{G}}}_{i}\left({{\boldsymbol{p}}}_{i}\right) $ 的Moore-Penrose广义逆矩阵;$ {e}_{il} $ ($ l={1,2},\cdots ,N $ )为非负常数.针对各个独立子系统构建辅助镇定律和对应的代价函数,并通过局部评判神经网络执行策略迭代算法,从而找到一组反馈镇定律
$ {{\boldsymbol{u}}}_{1}\left({{\boldsymbol{p}}}_{1}\right) $ ,$ {{\boldsymbol{u}}}_{2}\left({{\boldsymbol{p}}}_{2}\right), \cdots $ ,$ {{\boldsymbol{u}}}_{N}\left({{\boldsymbol{p}}}_{N}\right) $ ,使原互联系统(1)渐近稳定,且在控制过程中系统状态始终保持在预设的约束区间内.2 分散镇定系统设计
将耦合项
$ {Z}_{i}\left(\boldsymbol {p}\right) $ 沿$ {G}_{i}\left({{\boldsymbol{p}}}_{i}\right) $ 方向投影分解为匹配与非匹配的两项,如$$ \begin{split} {{\boldsymbol{Z}}}_{i}\left({\boldsymbol{p}}\right)=\;&{{\boldsymbol{G}}}_{i}\left({{\boldsymbol{p}}}_{i}\right){{\boldsymbol{G}}}_{i}^+\left({{\boldsymbol{p}}}_{i}\right){{\boldsymbol{K}}}_{i}\left({{\boldsymbol{p}}}_{i}\right){{\boldsymbol{D}}}_{i}\left({\boldsymbol{p}}\right)+\\ &\left({{\boldsymbol{I}}}_{{n}_{i}}-{{\boldsymbol{G}}}_{i}\left({{\boldsymbol{p}}}_{i}\right){{\boldsymbol{G}}}_{i}^+\left({{\boldsymbol{p}}}_{i}\right)\right){{\boldsymbol{K}}}_{i}\left({{\boldsymbol{p}}}_{i}\right){{\boldsymbol{D}}}_{i}\left({\boldsymbol{p}}\right),\end{split} $$ (11) 式中:
$ {{\boldsymbol{G}}}_{i}^{+}\left({{\boldsymbol{p}}}_{i}\right){{\boldsymbol{K}}}_{i}\left({{\boldsymbol{p}}}_{i}\right){{\boldsymbol{D}}}_{i}\left({\boldsymbol{p}}\right) $ 为$ {{\boldsymbol{Z}}}_{i}\left({\boldsymbol{p}}\right) $ 的匹配分量;$ {{\boldsymbol{I}}}_{{n}_{i}}\in {\mathbb{R}}^{{n}_{i}\times {n}_{i}} $ 为单位矩阵,系统(7)对应的独立子系统为$$ \dot{{{\boldsymbol{p}}}_{i}}={{\boldsymbol{F}}}_{i}\left({{\boldsymbol{p}}}_{i}\right)+{{\boldsymbol{G}}}_{i}\left({{\boldsymbol{p}}}_{i}\right){{\boldsymbol{u}}}_{i}+{{\boldsymbol{C}}}_{i}\left({{\boldsymbol{p}}}_{i}\right){{\boldsymbol{v}}}_{i}, $$ (12) 式中
$ {{\boldsymbol{C}}}_{i}\left({{\boldsymbol{p}}}_{i}\right)=\left({{\boldsymbol{I}}}_{{n}_{i}}-{{\boldsymbol{G}}}_{i}\left({{\boldsymbol{p}}}_{i}\right){{\boldsymbol{G}}}_{i}^{+}\left({{\boldsymbol{p}}}_{i}\right)\right){{\boldsymbol{K}}}_{i}\left({{\boldsymbol{p}}}_{i}\right) $ .辅助镇定律
$ {{\boldsymbol{v}}}_{i} $ 用于处理系统(7)中$ {Z}_{i}\left(\boldsymbol {p}\right) $ 的不匹配分量.独立子系统(12)对应的值函数设为$$ \begin{split} {V}_{i}\left({{p}}_{i}\left(t\right)\right)=\;&{\int }_{t}^{\infty }{r}_{i}\left({\boldsymbol{p}}_{i}\left(\tau \right),{\boldsymbol{u}}_{i}\left(\tau \right),{{\boldsymbol{v}}}_{i}\left(\tau \right)\right)+\\ &{\eta }_{i}{T}_{i}^{2}\left({\boldsymbol{p}}_{i}\left(\tau \right)\right){\rm{d}}\tau ,\end{split} $$ (13) 式中:
$ {r}_{i}\left({{\boldsymbol{p}}}_{i}\left(t\right),{{\boldsymbol{u}}}_{i}\left(t\right),{{\boldsymbol{v}}}_{i}\left(t\right)\right)={{\boldsymbol{p}}}_{i}^{\text{T}}{{\boldsymbol{Q}}}_{i}{{\boldsymbol{p}}}_{i}+{{\boldsymbol{u}}}_{i}^{\text{T}}{{\boldsymbol{R}}}_{i}{{\boldsymbol{u}}}_{i}+{{\boldsymbol{\varepsilon}} }_{i}{{\boldsymbol{v}}}_{i}^{\text{T}}{{\boldsymbol{v}}}_{i} $ ;$ {T}_{i}\left({{{p}}}_{i}\right)\geqslant \mathrm{max}\left\{{\alpha }_{i}\left(\|{\boldsymbol{p}}_{i}\|\right),{\beta }_{i}\left(\|{\boldsymbol{p}}_{i}\|\right)\right\} $ ,$ i=\mathrm{1,2},\cdots ,N$ ;$ {{\varepsilon }}_{i} $ 和$ {\mathrm{\boldsymbol{\eta} }}_{i} $ 为可调参数,$ {{\boldsymbol{Q}}}_{i}\in {\mathbb{R}}^{{n}_{i}\times {n}_{i}} $ 和$ {{\boldsymbol{R}}}_{i}\in {\mathbb{R}}^{{m}_{i}\times {m}_{i}} $ 为正定对称矩阵.代价函数(13)中$ {T}_{i}\left({{\boldsymbol{p}}}_{i}\right) $ 考虑耦合项$ {{\boldsymbol{Z}}}_{i}\left({\boldsymbol{p}}\right) $ 的范数上界,且$ {{\boldsymbol{Z}}}_{i}\left({\boldsymbol{p}}\right) $ 不出现在独立子系统(12)中.将系统(7)的分散镇定问题转化为系统(12)的最优控制问题,后续将通过最小化(13)补偿耦合项的影响.引入独立子系统后,需要寻找一对增广镇定律
$ \left({\boldsymbol{u}}_{i}^{*},{\boldsymbol {v}}_{i}^{*}\right) $ ,使得独立子系统(12)稳定,并最小化值函数(13),即$$ \left({{\boldsymbol{u}}}_{i}^{*},{{\boldsymbol{v}}}_{i}^{*}\right)=\mathrm{arg}\underset{\begin{array}{c}{{\boldsymbol{u}}}_{i}\in {\mathfrak{U}}\left({{\varOmega }}_{i}\right)\\ {\boldsymbol {v}}_{i}\in {\mathfrak{V}}\left({{\varOmega }}_{i}\right)\end{array}}{\mathrm{min}}{V}_{i}\left({{\boldsymbol{p}}}_{i}\left(t\right)\right), $$ (14) 式中
$ \mathfrak{U}\left({{\varOmega }}_{i}\right) $ 和$ \mathfrak{V}\left({{\varOmega }}_{i}\right) $ 分别为控制律$ {\boldsymbol{u}}_{i} $ 和$ {\boldsymbol{v}}_{i} $ 的可容许镇定控制集合.当代价函数$ {V}_{i}\left({\boldsymbol{p}}_{i}\left(t\right)\right) $ 达到最小,即$$ \begin{split}{V}_{i}^{*}\left({\boldsymbol{p}}_{i}\left(t\right)\right)=\;&{\int }_{t}^{{\infty }}\left[{r}_{i}\left({{\boldsymbol{p}}}_{i}^{*}\left({\tau }\right),{{\boldsymbol{u}}}_{i}^{*}\left({\tau }\right),{{\boldsymbol{v}}}_{i}^{*}\left({\tau }\right)\right)+\right.\\ &\left.{\eta }_{i}{T}_{i}^{2}\left({{\boldsymbol{p}}}_{i}^{*}\left(\tau \right)\right)\right]{\rm{d}}\tau ,\end{split} $$ (15) 其满足
$$ \begin{split} &\nabla {{V}_{i}^{*}}^{\text{T}}\left({{\boldsymbol{p}}}_{i}\right)\left({\boldsymbol{F}}_{i}\left({{\boldsymbol{p}}}_{i}\right)+{{\boldsymbol{G}}}_{i}\left({{\boldsymbol{p}}}_{i}\right){{\boldsymbol{u}}}_{i}+{{\boldsymbol{C}}}_{i}\left({{\boldsymbol{p}}}_{i}\right){{\boldsymbol{v}}}_{i}\right) +\\ &\quad\quad\quad\;\;\;{r}_{i}\left({{\boldsymbol{p}}}_{i},{{\boldsymbol{u}}}_{i},{{\boldsymbol{v}}}_{i}\right)+{{\eta }}_{i}{T}_{i}^{2}\left({{\boldsymbol{p}}}_{i}\right)=0.\end{split} $$ (16) 独立子系统(12)的哈密顿函数为
$$ \begin{split} &H\left(\nabla {{\boldsymbol{V}}}_{i}^{\text{T}},{{\boldsymbol{p}}}_{i},{{\boldsymbol{u}}}_{i},{{\boldsymbol{v}}}_{i}\right)=\nabla {{\boldsymbol{V}}}_{i}^{\text{T}}\left({{\boldsymbol{p}}}_{i}\right)\left({{\boldsymbol{F}}}_{i}\left({{\boldsymbol{p}}}_{i}\right)+{{\boldsymbol{G}}}_{i}\left({{\boldsymbol{p}}}_{i}\right){{\boldsymbol{u}}}_{i}+\right.\\ &\quad\quad\quad\quad \left.{{\boldsymbol{C}}}_{i}\left({{\boldsymbol{p}}}_{i}\right){{\boldsymbol{v}}}_{i}\right)+{r}_{i}\left({{\boldsymbol{p}}}_{i},{{\boldsymbol{u}}}_{i},{{\boldsymbol{v}}}_{i}\right)+{{\eta }}_{i}{T}_{i}^{2}\left({{\boldsymbol{p}}}_{i}\right).\end{split} $$ (17) 根据贝尔曼最优性原理,可知
$$ \underset{\begin{array}{c}{{\boldsymbol {u}}}_{i}\in {\mathfrak{U}}\left({{\varOmega }}_{i}\right)\\ {\boldsymbol {v}}_{i}\in {\mathfrak{V}}\left({{\varOmega }}_{i}\right)\end{array}}{\mathrm{min}}H\left({\boldsymbol{\nabla}} {\boldsymbol{V}}_{i}^{\text{T}},{\boldsymbol{p}}_{i},{\boldsymbol{u}}_{i},{{\boldsymbol{v}}}_{i}\right)=0. $$ (18) 由式(13)和(18)可得,独立子系统(12)的最优反馈控制律
$ \left({\boldsymbol{u}}_{i}^{*},{{\boldsymbol{v}}}_{i}^{*}\right) $ 表达式为$$ {\boldsymbol{u}}_{i}^{*}=-\frac{1}{2}{{\boldsymbol{R}}}_{i}^{-1}{{\boldsymbol{G}}}_{i}^{\text{T}}\left({{\boldsymbol{p}}}_{i}\right){\boldsymbol{\nabla}} {\boldsymbol{V}}_{i}^{*}\left({{\boldsymbol{p}}}_{i}\right), $$ (19) $${{\boldsymbol{v}}}_{i}^{*}=-\frac{1}{2{\varepsilon }_{i}}{{\boldsymbol{C}}}_{i}^{\text{T}}\left({{\boldsymbol{p}}}_{i}\right){\boldsymbol{\nabla}} {\boldsymbol{V}}_{i}^{*}\left({{\boldsymbol{p}}}_{i}\right). $$ (20) 3 神经网络求解
3.1 策略迭代算法
由于HJB方程中存在偏微分项
$ {{\nabla}} {{V}}_{i}^{*}\left({{{p}}}_{i}\right) $ ,使其难以直接求解,本节将采用策略迭代算法对其进行近似求解.研究证明,该算法在迭代次数趋于无穷时,代价函数和镇定律均收敛到最优[21].记
$$ {\mathcal{G}}_{i}\left({{\boldsymbol{p}}}_{i}\right)=\left[{{\boldsymbol{G}}}_{i}\left({{\boldsymbol{p}}}_{i}\right),{{\boldsymbol{C}}}_{i}\left({{\boldsymbol{p}}}_{i}\right)\right], $$ (21) $$ {\boldsymbol{\mu }}_{i}\left({{\boldsymbol{p}}}_{i}\right)={\left[{\boldsymbol{u}}_{i}^{\text{T}}\left({{\boldsymbol{p}}}_{i}\right),{{\boldsymbol{v}}}_{i}^{\text{T}}\left({{\boldsymbol{p}}}_{i}\right)\right]}^{\text{T}}.$$ (22) 则独立子系统(12)可表示为
$$ {\dot{{\boldsymbol{p}}}}_{i}={{\boldsymbol{F}}}_{i}\left({{\boldsymbol{p}}}_{i}\right)+{\mathcal{G}}_{i}\left({{\boldsymbol{p}}}_{i}\right){\boldsymbol{\mu }}_{i}\left({{\boldsymbol{p}}}_{i}\right).$$ (23) 式(13)中的
$ {r}_{i}\left({\boldsymbol{p}}_{i}\left(t\right),{\boldsymbol{u}}_{i}\left(t\right),{{\boldsymbol{v}}}_{i}\left(t\right)\right) $ 可表示为$$ {{\boldsymbol{r}}}_{i}\left({\boldsymbol{p}}_{i}\left(t\right),{\boldsymbol{\mu }}_{i}\left(t\right)\right)={\boldsymbol{p}}_{i}^{\text{T}}{\boldsymbol{Q}}_{i}{\boldsymbol{p}}_{i}+{\boldsymbol{\mu }}_{i}^{{\rm{T}}}{\mathcal{R}}_{i}{\boldsymbol{\mu }}_{i}, $$ (24) 式中
$ {\mathcal{R}}_{i}={\text{diag}}\left\{{{\boldsymbol{R}}}_{i},{\varepsilon }_{i}{{\boldsymbol{I}}}_{{n}_{i}}\right\} $ .下面,采用策略迭代算法逼近各个独立子系统的最优镇定律.针对第
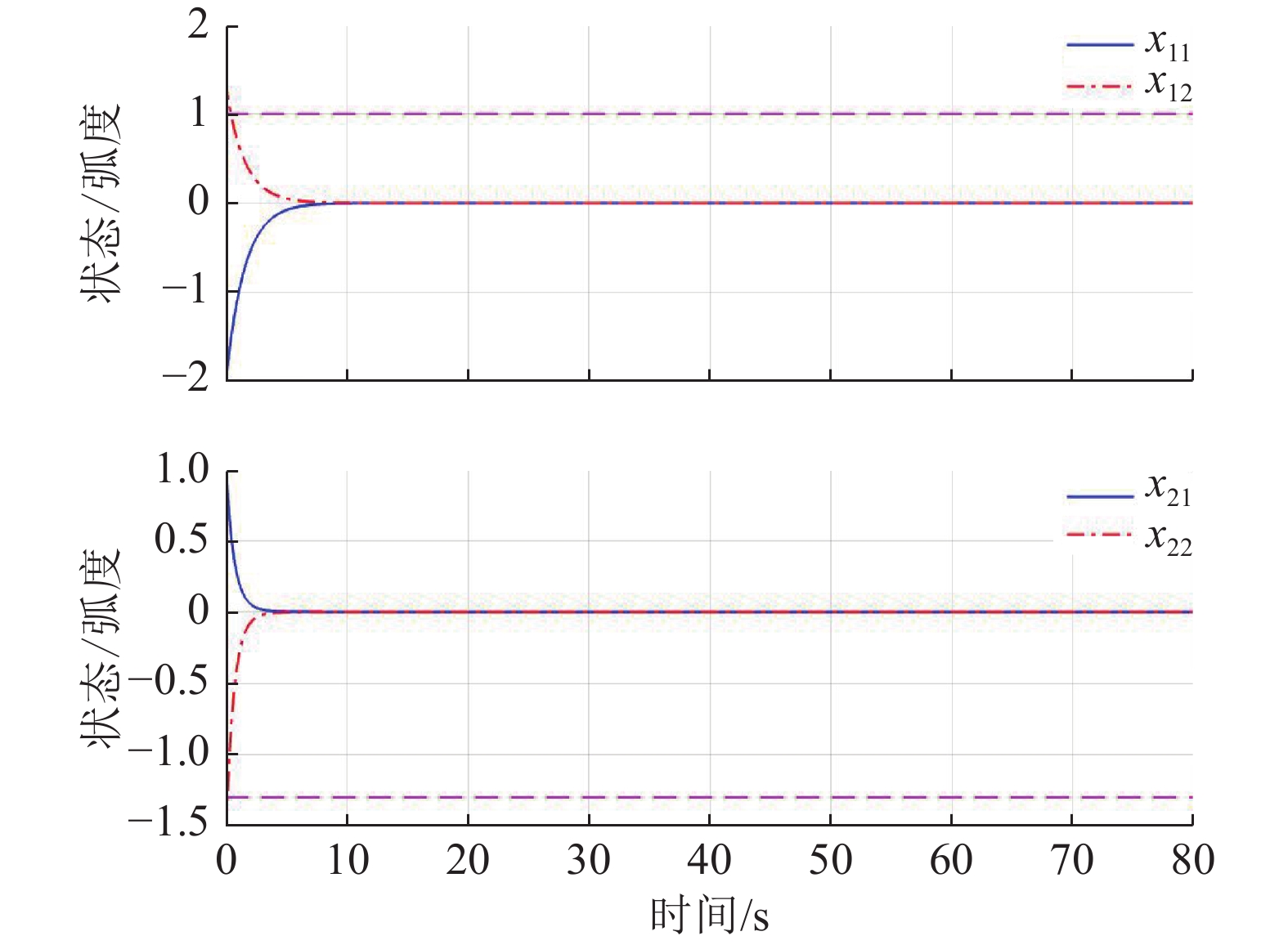
$ i $ 个独立子系统选择一个初始可容许镇定律$ {\mathrm{\boldsymbol{\mu} }}_{i}^{\left(0\right)}={\left[{{{\boldsymbol{u}}}_{i}^{\left(0\right)}}^{\text{T}}\left({{\boldsymbol{p}}}_{i}\right),{{{\boldsymbol{v}}}_{i}^{\left(0\right)}}^{\text{T}}\left({{\boldsymbol{p}}}_{i}\right)\right]}^{\text{T}} $ ,其中$ {{\boldsymbol{u}}}_{i}^{\left(0\right)}\in \mathfrak{U}\left({{\varOmega }}_{i}\right) $ ,$ {{\boldsymbol{v}}}_{i}^{\left(0\right)}\in \mathfrak{V}\left({{\varOmega }}_{i}\right) $ .然后,通过下面两式依次重复进行策略评价和策略更新,即$$ \begin{split} &{\left({\boldsymbol{\nabla}} {\boldsymbol{V}}_{i}^{\left(q+1\right)}\left({{\boldsymbol{p}}}_{i}\right)\right)}^{\text{T}}\left({\boldsymbol{F}}_{i}\left({{\boldsymbol{p}}}_{i}\right)+{\mathcal{G}}_{i}\left({{\boldsymbol{p}}}_{i}\right){\boldsymbol{\mu }}_{i}^{\left(q\right)}\left({{\boldsymbol{p}}}_{i}\right)\right)+\\& \qquad\quad {r}_{i}\left({\boldsymbol{p}}_{i},{\boldsymbol{\mu }}_{i}^{\left(q\right)}\left({{\boldsymbol{p}}}_{i}\right)\right)+{\eta }_{i}{T}_{i}^{2}\left({{{\boldsymbol {p}}}}_{i}\right)=0,\end{split} $$ (25) $$ {\boldsymbol{\mu }}_{i}^{\left(q+1\right)}=-\frac{1}{2}{\mathcal{R}}^{-1}\left({{\boldsymbol{p}}}_{i}\right){\mathcal{G}}_{i}^{\text{T}}\left({{\boldsymbol{p}}}_{i}\right){\boldsymbol{\nabla}} {\boldsymbol{V}}_{i}^{\left(q+1\right)}\left({{\boldsymbol{p}}}_{i}\right). $$ (26) 直到迭代至第
$ q $ 步时代价函数收敛到设定的误差范围$ \mathrm{\vartheta } $ ,迭代过程如图1所示.3.2 局部评判神经网络实现
神经网络具有通用近似能力,因而可以用来估计子系统的值函数,进而在线求解HJB方程(18).本文系统模型已知,因此可以舍弃执行神经网络以简化神经网络结构,通过局部评判神经网络即可估计子系统的值函数(15).最优代价函数
$$ {V}_{i}^{*}\left({{\boldsymbol{p}}}_{i}\right)={\boldsymbol{W}}_{ci}^{\text{T}}{{{\boldsymbol{\sigma}} }}_{ci}\left({{\boldsymbol{p}}}_{i}\right)+{{{\zeta} }}_{ci}\left({{\boldsymbol{p}}}_{i}\right), $$ (27) 式中:
$ {\boldsymbol{W}}_{ci}\in {\mathbb{R}}^{{l}_{ci}} $ 是未知的理想权重;$ {{\boldsymbol{\sigma}} }_{ci}\left({{\boldsymbol{p}}}_{i}\right)\in {\mathbb{R}}^{{l}_{ci}} $ 是可导并连续的激活函数,且$ {{\boldsymbol{\sigma}} }_{ci}\left(0\right)=0 $ ;$ {l}_{ci} $ 是局部评判神经网络中神经元的数量;$ {\mathrm{{\zeta} }}_{ci}\left({{\boldsymbol{p}}}_{i}\right) $ 是重构误差.将式(27)对$ {\boldsymbol{p}}_{i} $ 求梯度可得$$ {\boldsymbol{\nabla}} {{\boldsymbol{V}}}_{i}^{*}\left({{\boldsymbol{p}}}_{i}\right)=\nabla {{\boldsymbol{\sigma}} }_{ci}^{\text{T}}\left({{\boldsymbol{p}}}_{i}\right){\boldsymbol{W}}_{ci}+\nabla {{\zeta} }_{ci}\left({{\boldsymbol{p}}}_{i}\right), $$ (28) 式中:
$ \nabla \left(\cdot\right) $ 表示求梯度运算.由式(19)~(22)、(28),可将增广控制律$ {\boldsymbol{\mu }}_{i}^{*}\left({{\boldsymbol{p}}}_{i}\right) $ 重构为$$ {\boldsymbol{\mu }}_{i}^{*}\left({{\boldsymbol{p}}}_{i}\right)=-\frac{1}{2}{\mathcal{R}}_{i}^{-1}{\mathcal{G}}_{i}^{\mathrm{T}}\left({{\boldsymbol{p}}}_{i}\right)\nabla {{{\boldsymbol{\sigma}} }}_{ci}^{\text{T}}\left({{\boldsymbol{p}}}_{i}\right){{\boldsymbol{W}}}_{ci}+{{{{\boldsymbol{\zeta}}} }}_{{{\mu }}_{i}^{*}}\left({{\boldsymbol{p}}}_{i}\right), $$ (29) 式中
$ {\boldsymbol{\zeta} }_{{\boldsymbol{\mu }}_{i}^{*}}\left({{\boldsymbol{p}}}_{i}\right)=-\dfrac{1}{2}{\mathcal{R}}_{i}^{-1}{\mathcal{G}}_{i}^{\mathrm{T}}\left({{\boldsymbol{p}}}_{i}\right)\nabla {\boldsymbol{\zeta} }_{\text{ci}}\left({{\boldsymbol{p}}}_{i}\right) $ .HJB方程(18)可化为$$ \begin{split} &{\eta }_{i}{T}_{i}^{2}\left({{\boldsymbol{p}}}_{i}\right)+{\boldsymbol{p}}_{i}^{\text{T}}{\boldsymbol{Q}}_{i}{\boldsymbol{p}}_{i}+{{\boldsymbol{\mu }}_{i}^{*}}^{\text{T}}\left({{\boldsymbol{p}}}_{i}\right){\mathcal{R}}_{i}{\boldsymbol{\mu }}_{i}^{*}\left({{\boldsymbol{p}}}_{i}\right)+\\ &\qquad{\left(\nabla {{\boldsymbol{V}}}_{i}^{*}\left({{\boldsymbol{p}}}_{i}\right)\right)}^{\text{T}}\left({\boldsymbol{F}}_{i}\left({{\boldsymbol{p}}}_{i}\right)+{\mathcal{G}}_{i}\left({{\boldsymbol{p}}}_{i}\right){\boldsymbol{\mu }}_{i}^{*}\left({{\boldsymbol{p}}}_{i}\right)\right)=0.\end{split} $$ (30) 由于局部评判神经网络的理想权重
$ {{W}}_{ci} $ 未知,因此将其估计值记为$ {\widehat{\boldsymbol{W}}}_{ci} $ ,因此最优代价函数的估计值记为$ \widehat{{V}_{i}}\left({{\boldsymbol{p}}}_{i}\right) $ .则$$ \widehat{{V}_{i}}\left({{{{\boldsymbol{p}}}}}_{i}\right)={\widehat{\boldsymbol{W}}}_{ci}^{{\rm{T}}}{{{\boldsymbol{\sigma}} }}_{ci}\left({{\boldsymbol{p}}}_{i}\right), $$ (31) $$ {\widehat{\boldsymbol{\mu} }}_{i}\left({{\boldsymbol{p}}}_{i}\right)=-\frac{1}{2}{\mathcal{R}}_{i}^{-1}{\mathcal{G}}_{i}^{\mathrm{T}}\left({{\boldsymbol{p}}}_{i}\right)\nabla {{\boldsymbol{\sigma}} }_{ci}^{\text{T}}\left({{\boldsymbol{p}}}_{i}\right){\widehat{\boldsymbol{W}}}_{ci}. $$ (32) 由式(17)和(31)可知,近似的哈密顿函数为
$$\widehat{H}\left({\boldsymbol{\nabla}} {\widehat{\boldsymbol{V}}}_{i},{\boldsymbol{p}}_{i},{\widehat{\boldsymbol{\mu} }}_{i}\right)={\eta }_{i}{T}_{i}^{2}\left({{\boldsymbol{p}}}_{i}\right)+{r}_{i}\left({\boldsymbol{p}}_{i},{\widehat{\boldsymbol{\mu} }}_{i}\right)+{\widehat{\boldsymbol{W}}}_{ci}^{{\rm{T}}}{{{\boldsymbol{\phi }}}}_{i}, $$ (33) 式中
$ {\mathrm{{\boldsymbol{\phi }}}}_{i}={\boldsymbol{\nabla}} {\mathrm{{\boldsymbol{\sigma}} }}_{ci}\left({{\boldsymbol{p}}}_{i}\right)\left({\boldsymbol{F}}_{i}\left({{\boldsymbol{p}}}_{i}\right)+{\mathcal{G}}_{i}\left({{\boldsymbol{p}}}_{i}\right){\widehat{\boldsymbol{\mu} }}_{i}\left({{\boldsymbol{p}}}_{i}\right)\right) $ .定义哈密顿函数的估计误差为
$$ \begin{split} &{e}_{ci}={\widehat{H}}_{i}\left(\nabla {\widehat{\boldsymbol{V}}}_{i},{\boldsymbol{p}}_{i},{\widehat{\boldsymbol{\mu} }}_{i}\right)-{H}_{i}\left(\nabla {{\boldsymbol{V}}}_{i}^{*},{\boldsymbol{p}}_{i},{{{\boldsymbol{\mu}} }}_{i}^{*}\right) =\\ &\qquad{{\eta }}_{i}{T}_{i}^{2}\left({{\boldsymbol{p}}}_{i}\right)+{r}_{i}\left({\boldsymbol{p}}_{i},{\widehat{\boldsymbol{\mu} }}_{i}\right)+{\widehat{{\boldsymbol{W}}}}_{ci}^{\mathrm{T}}{{{\boldsymbol{\phi}} }}_{i}.\end{split} $$ (34) 对局部评判神经网络权重
$ {\widehat{\boldsymbol{W}}}_{ci} $ 训练的目标是使其收敛到理想权重$ {\boldsymbol{W}}_{ci} $ .因此,定义目标函数$ {E}_{ci}=\dfrac{1}{2}{{\rm{e}}}_{ci}^{\text{T}}{{\rm{e}}}_{ci} $ ,并通过梯度下降法(35)训练局部评判神经网络权重以最小化$ {E}_{ci} $ ,则局部评判神经网络权重的更新律为$$ {\dot{\widehat{{\boldsymbol{W}}}}}_{ci}=-\frac{{\gamma }_{ci}}{{\left(1+{\boldsymbol{\phi} }_{i}^{\text{T}}{\boldsymbol{\phi} }_{i}\right)}^{2}}\frac{\partial {E}_{ci}}{\partial {\widehat{{\boldsymbol{W}}}}_{ci}} =-{\gamma }_{ci}\frac{{\boldsymbol{\phi} }_{i}{{\rm{e}}}_{ci}}{{\left(1+{\boldsymbol{\phi} }_{i}^{\text{T}}{\boldsymbol{\phi} }_{i}\right)}^{2}}, $$ (35) 式中
$ {\gamma }_{ci} > 0 $ 为学习率,$ {\left(1+{\boldsymbol{\phi} }_{i}^{\text{T}}{\boldsymbol{\phi} }_{i}\right)}^{2} $ 用于归一化.定义局部评判神经网络权重误差为
$ {\widetilde{{\boldsymbol{W}}}}_{ci}={{\boldsymbol{W}}}_{ci}-{\widehat{{\boldsymbol{W}}}}_{ci} $ .将其对时间求导,结合式(35)可得$${\dot{\widetilde{{\boldsymbol{W}}}}}_{ci}=-{{\gamma }}_{ci}{{\boldsymbol{\psi}}}_{i}{{\boldsymbol{\psi}}}_{i}^{\text{T}}{\widetilde{{\boldsymbol{W}}}}_{ci}+\frac{{{\gamma }}_{ci}{{\boldsymbol{\psi}}}_{i}{{{\zeta} }}_{Hi}\left({{\boldsymbol{p}}}_{i}\right)}{1+{{\boldsymbol{\phi}} }_{i}^{\text{T}}{{\boldsymbol{\phi}} }_{i}},$$ (36) 式中:
$$\begin{split} &{{\boldsymbol{\psi}}}_{i}=\frac{{{\boldsymbol{\phi}} }_{i}}{1+{{\boldsymbol{\phi}} }_{i}^{\text{T}}{{\boldsymbol{\phi}} }_{i}} , \\ &{{\zeta} }_{Hi}\left({{\boldsymbol{p}}}_{i}\right)=-\nabla {{\zeta} }_{ci}^{\text{T}}\left({{\boldsymbol{p}}}_{i}\right)\left({\boldsymbol{F}}_{i}\left({{\boldsymbol{p}}}_{i}\right)+{\mathcal{G}}_{i}\left({{\boldsymbol{p}}}_{i}\right){\widehat{\boldsymbol{\mu} }}_{i}\left({{\boldsymbol{p}}}_{i}\right)\right). \end{split}$$ 3.3 稳定性分析
假设4
$ {\mathcal{G}}_{i}\left({{\boldsymbol{p}}}_{i}\right) $ 、$ {\mathrm{{\boldsymbol{\sigma}} }}_{ci}\left({{\boldsymbol{p}}}_{i}\right) $ 、$ \nabla {\mathrm{{\boldsymbol{\sigma}} }}_{ci}\left({{\boldsymbol{p}}}_{i}\right) $ 、$ {\mathrm{\boldsymbol{\zeta} }}_{ci}\left({{\boldsymbol{p}}}_{i}\right) $ 、$ \nabla {\mathrm{\boldsymbol{\zeta} }}_{ci}\left({{\boldsymbol{p}}}_{i}\right) $ 、$ {\mathrm{\boldsymbol{\zeta} }}_{Hi}\left({{\boldsymbol{p}}}_{i}\right) $ 均为范数有界的,即满足$ \left\|{\mathcal{G}}_{i} \left({{\boldsymbol{p}}}_{i}\right) \right\|\leqslant{\lambda }_{1} $ ,$ |\left|{{\boldsymbol{\sigma}} }_{ci} \left({{\boldsymbol{p}}}_{i}\right) \right\|\leqslant{\lambda }_{2} $ ,$ |\left|\nabla {{\boldsymbol{\sigma}} }_{ci} \left({{\boldsymbol{p}}}_{i}\right) \right\|\leqslant{\lambda }_{3} $ ,$ \|{\boldsymbol{\zeta} }_{ci} \left({{\boldsymbol{p}}}_{i}\right) \|\leqslant {\lambda }_{4} $ ,$ \|\nabla {\boldsymbol{\zeta} }_{ci}\left({{\boldsymbol{p}}}_{i}\right)||\leqslant{\lambda }_{5} $ ,$ \|{\boldsymbol{\zeta} }_{{H}_{i}}\left({{\boldsymbol{p}}}_{i}\right)\|\leqslant{\lambda }_{6} $ , 其中,$ {\lambda }_{1},{\lambda }_{2},\cdots ,{\lambda }_{6} $ 均为正常数.假设5
$ {\mathrm{\psi }}_{i} $ 满足持续激励条件,即存在$ {\varrho }_{2}\geqslant{\varrho }_{1} > 0 $ ,$ T > 0 $ ,使$$ {\varrho }_{1}{\boldsymbol{I}}_{{l}_{ci}}\leqslant{\int }_{t}^{t+T}{{\boldsymbol{\psi}}}_{i}\left(\tau \right){{\boldsymbol{\psi}}}_{i}^{\text{T}}\left(\tau \right){\rm{d}}\tau \leqslant{\varrho }_{2}{\boldsymbol{I}}_{{l}_{ci}},\forall t\geqslant0. $$ 定理1 对于第
$ i $ 个独立子系统(12),若假设1~5成立,初始镇定律满足$ {{\boldsymbol{u}}}_{i}^{\left(0\right)}\in \mathfrak{U}\left({{\varOmega }}_{i}\right) $ ,$ {{\boldsymbol{v}}}_{i}^{\left(0\right)}\in \mathfrak{V}\left({{\varOmega }}_{i}\right) $ ,局部评判神经网络的权重由式(35)更新,且满足$$ {{\gamma }}_{ci}\geqslant\frac{{\lambda }_{1}^{2}{\lambda }_{3}^{2}}{{\lambda }_{\mathrm{m}\mathrm{i}\mathrm{n}}\left({{\boldsymbol{\psi}}}_{i}{{\boldsymbol{\psi}}}_{i}^{\mathrm{T}}\right){\lambda }_{\mathrm{m}\mathrm{i}\mathrm{n}}\left({\mathcal{R}}_{i}\right)}, $$ (37) 则独立子系统状态
$ {\boldsymbol{p}}_{i} $ 和权重估计误差$ {\widetilde{{\boldsymbol{W}}}}_{ci} $ 是最终一致有界的.证明:选取Lyapunov函数
$$ {\mathcal{L}}_{i}\left(t\right)={V}_{i}^{*}\left({\boldsymbol{p}}_{i}\left(t\right)\right)+\frac{1}{2}{\widetilde{{\boldsymbol{W}}}}_{ci}^{\mathrm{T}}{\widetilde{{\boldsymbol{W}}}}_{ci}, $$ 记
$ {\mathcal{L}}_{i1}\left(t\right)={V}_{i}^{*}\left({\boldsymbol{p}}_{i}\left(t\right)\right) $ ,$ {\mathcal{L}}_{i2}\left(t\right)=\dfrac{1}{2}{\widetilde{{\boldsymbol{W}}}}_{ci}^{\mathrm{T}}{\widetilde{{\boldsymbol{W}}}}_{ci} $ .将$ {\widehat{\boldsymbol{\mu} }}_{i} $ 代入式(23),得到$ \dot{{\boldsymbol{p}}_{i}}={{\boldsymbol{F}}}_{i}\left({{\boldsymbol{p}}}_{i}\right)+{\mathcal{G}}_{i}\left({{\boldsymbol{p}}}_{i}\right){\widehat{\boldsymbol{\mu} }}_{i} $ ,其代价函数导数表示为$$ \dot{{V}_{i}^{*}}\left({{\boldsymbol{p}}}_{i}\right)=\nabla {{V}_{i}^{*}}^{\text{T}}\left({{\boldsymbol{p}}}_{i}\right)\left({\boldsymbol{F}}_{i}\left({{\boldsymbol{p}}}_{i}\right)+{\mathcal{G}}_{i}\left({{\boldsymbol{p}}}_{i}\right){\widehat{{{\boldsymbol{\mu}} }}}_{i}\right) .$$ (38) 结合式(29)、(30)和(38),可得
$$ \begin{split} &\dot{{\mathcal{L}}_{i1}}\left(t\right)=\nabla {{V}_{i}^{*}}^{\text{T}}\left({{\boldsymbol{p}}}_{i}\right)\left({\boldsymbol{F}}_{i}\left({{\boldsymbol{p}}}_{i}\right)+{\mathcal{G}}_{i}\left({{\boldsymbol{p}}}_{i}\right){\widehat{\boldsymbol{\mu} }}_{i}\left({{\boldsymbol{p}}}_{i}\right)\right)=\\ &-{\mathrm{{\eta} }}_{i}{T}_{i}^{2}\left({{\boldsymbol{p}}}_{i}\right)-{\boldsymbol{p}}_{i}^{\text{T}}{\boldsymbol{Q}}_{i}{\boldsymbol{p}}_{i}+{{{\mathrm{\boldsymbol{\mu} }}_{i}^{*}}^{\text{T}}\mathcal{R}}_{i}{\mathrm{\boldsymbol{\mu} }}_{i}^{*}-2{{\boldsymbol{\mu }}_{i}^{*}}^{\mathrm{T}}{\mathcal{R}}_{i}{\widehat{\boldsymbol{\mu} }}_{i}= \\ &\|{\mathcal{R}}_{i}^{\frac{1}{2}}\left({{\boldsymbol{\mu }}}_{i}^{*}-{\widehat{\boldsymbol{\mu} }}_{i}\right)\|^{2}-{\mathrm{{\eta} }}_{i}{T}_{i}^{2}\left({{\boldsymbol{p}}}_{i}\right)-{r}_{i}\left({\boldsymbol{p}}_{i},{\widehat{\boldsymbol{\mu} }}_{i}\right).\end{split} $$ (39) 记
$ {\mathrm{\Gamma }}_{i1}= \|{\mathcal{R}}_{i}^{\frac{1}{2}}\left({{\boldsymbol{\mu }}}_{i}^{*}-{\widehat{\boldsymbol{\mu} }}_{i}\right){\|}^{2}$ ,将式(29)、(32)代入式(39),并结合不等式$ \dfrac{\|a+b{\|}^{2}}{2}\leqslant\|a{\|}^{2}+\|b{\|}^{2}$ ,$ \forall a,b\in \mathbb{R} $ ,可得$$ \begin{split} &{{\Gamma }}_{i1}=\|\frac{1}{2}{\mathcal{R}}_{i}^{-\frac{1}{2}}{\mathcal{G}}_{i}^{\mathrm{T}}\left({{\boldsymbol{p}}}_{i}\right)\nabla {{\boldsymbol{\sigma}} }_{ci}^{\text{T}}\left({{\boldsymbol{p}}}_{i}\right){\widetilde{{\boldsymbol{W}}}}_{ci}\left({{\boldsymbol{p}}}_{i}\right)-{\mathcal{R}}_{i}^{\frac{1}{2}}{\boldsymbol{\zeta} }_{{\boldsymbol{\mu }}_{i}^{*}}\left({{\boldsymbol{p}}}_{i}\right){\|}^{2} \leqslant\\ &\qquad\frac{1}{2}\|{\mathcal{R}}_{i}^{-\frac{1}{2}}{\mathcal{G}}_{i}^{\mathrm{T}}\left({{\boldsymbol{p}}}_{i}\right)\nabla {{{\boldsymbol{\sigma}} }}_{ci}^{\text{T}}\left({{\boldsymbol{p}}}_{i}\right){\widetilde{{\boldsymbol{W}}}}_{ci}\left({{\boldsymbol{p}}}_{i}\right){\|}^{2}+2\|{\mathcal{R}}_{i}^{\frac{1}{2}}{{\boldsymbol{\zeta} }}_{{{\mu }}_{i}^{*}}\left({{\boldsymbol{p}}}_{i}\right){\|}^{2}.\end{split} $$ (40) 因此,结合假设4,式(39)可进一步化为
$$ \begin{split} &{\mathcal{L}}_{i1}\left(t\right)\leqslant-{\mathrm{{\eta} }}_{i}{T}_{i}^{2}\left({{\boldsymbol{p}}}_{i}\right)-{r}_{i}\left({\boldsymbol{p}}_{i},{\widehat{\boldsymbol{\mu} }}_{i}\right)+2\|{\mathcal{R}}_{i}^{\frac{1}{2}}{\mathrm{\boldsymbol{\zeta} }}_{{\mathrm{\boldsymbol{\mu} }}_{i}^{*}}\left({{\boldsymbol{p}}}_{i}\right)|{|}^{2}+\\ &\frac{1}{2}\|{\mathcal{R}}_{i}^{-\frac{1}{2}}{\mathcal{G}}_{i}^{\mathrm{T}}\left({{\boldsymbol{p}}}_{i}\right)\nabla {\mathrm{{\boldsymbol{\sigma}} }}_{ci}^{\text{T}}\left({{\boldsymbol{p}}}_{i}\right){\widetilde{{\boldsymbol{W}}}}_{ci}\left({{\boldsymbol{p}}}_{i}\right){\|}^{2}\leqslant\\ &-{\lambda }_{\mathrm{m}\mathrm{i}\mathrm{n}}\left({\boldsymbol{Q}}_{i}\right)\|{\boldsymbol{p}}_{i}{\|}^{2}+\frac{{\lambda }_{1}^{2}{\lambda }_{5}^{2}}{2{\lambda }_{\mathrm{m}\mathrm{i}\mathrm{n}}\left({\mathcal{R}}_{i}\right)}+\frac{{\lambda }_{1}^{2}{\lambda }_{3}^{2}}{2{\lambda }_{\mathrm{m}\mathrm{i}\mathrm{n}}\left({\mathcal{R}}_{i}\right)}\|{\widetilde{{\boldsymbol{W}}}}_{ci}\left({{\boldsymbol{p}}}_{i}\right){\|}^{2}.\end{split} $$ (41) 由式(36)可得
$$ \begin{split} \dot{{\mathcal{L}}_{i2}}\left(t\right)=&-{\mathrm{\gamma }}_{ci}{\widetilde{{\boldsymbol{W}}}}_{{c}{i}}^{\mathrm{T}}\left({{\boldsymbol{p}}}_{i}\right){{\boldsymbol{\psi}}}_{i}{{\boldsymbol{\psi}}}_{i}^{\text{T}}{\widetilde{{\boldsymbol{{\boldsymbol{W}}}}}}_{ci}\left({{\boldsymbol{p}}}_{i}\right) +\\ &{\gamma }_{ci}\frac{{\widetilde{{\boldsymbol{W}}}}_{{c}{i}}^{\mathrm{T}}\left({{\boldsymbol{p}}}_{i}\right){{\boldsymbol{\psi}}}_{i}}{1+{\boldsymbol{\varphi }}_{i}^{\mathrm{T}}{\boldsymbol{\varphi }}_{i}}{\boldsymbol{\zeta} }_{{H}_{i}}\left({{\boldsymbol{p}}}_{i}\right),\end{split} $$ (42) 式中
$$ \begin{split} &{\gamma }_{ci}\frac{{\widetilde{{\boldsymbol{W}}}}_{ci}^{\mathrm{T}}\left({{\boldsymbol{p}}}_{i}\right){{\boldsymbol{\psi}}}_{i}}{1+{\boldsymbol{\varphi }}_{i}^{\text{T}}{\boldsymbol{\varphi }}_{i}}{\boldsymbol{\zeta} }_{{H}_{i}}\left({{\boldsymbol{p}}}_{i}\right) \leqslant |{\gamma }_{ci}{\widetilde{{\boldsymbol{W}}}}_{ci}^{{\rm{T}}}\left({{\boldsymbol{p}}}_{i}\right){{\boldsymbol{\psi}}}_{i}{\boldsymbol{\zeta} }_{{H}_{i}}\left({{\boldsymbol{p}}}_{i}\right)|\leqslant\\&\qquad\frac{{\gamma }_{ci}}{2}{\widetilde{{\boldsymbol{W}}}}_{ci}^{{\rm{T}}}\left({{\boldsymbol{p}}}_{i}\right){{\boldsymbol{\psi}}}_{i}{{\boldsymbol{\psi}}}_{i}^{\text{T}}{\widetilde{{\boldsymbol{W}}}}_{ci}\left({{\boldsymbol{p}}}_{i}\right)+\frac{{\gamma }_{ci}}{2}{\boldsymbol{\zeta} }_{{H}_{i}}^{\text{T}}{\boldsymbol{\zeta} }_{{H}_{i}}. \end{split}$$ 由式(42)和假设4可得
$$ \dot{{\mathcal{L}}_{i2}}\left(t\right)\leqslant-\frac{{\gamma }_{ci}}{2}{\lambda }_{\min}\left({{\boldsymbol{\psi}} }_{i}{{\boldsymbol{\psi}} }_{i}^{\text{T}}\right)||{\widetilde{{\boldsymbol{W}}}}_{ci}\left({{\boldsymbol{p}}}_{i}\right){\|}^{2}+\frac{{\gamma }_{ci}}{2}{\lambda }_{6}^{2}. $$ (43) 联立式(41)和(43)可得
$$ \begin{split} {\mathcal{L}}_{i}\left(t\right)=&{\mathcal{L}}_{i1}\left(t\right)+{\mathcal{L}}_{i2}\left(t\right)\leqslant\\& -{\mathrm{\lambda }}_{\min}\left({{\boldsymbol{Q}}}_{i}\right)\|{{\boldsymbol{p}}}_{i}{\|}^{2}+\frac{{\mathrm{\lambda }}_{1}^{2}{\mathrm{\lambda }}_{5}^{2}}{2{\mathrm{\lambda }}_{\mathrm{m}\mathrm{i}\mathrm{n}}\left({\mathcal{R}}_{i}\right)}+\frac{{\mathrm{\gamma }}_{ci}{\mathrm{\lambda }}_{6}^{2}}{2} -\\& \left(\frac{{\gamma }_{ci}}{2}{\lambda }_{\mathrm{m}\mathrm{i}\mathrm{n}}\left({{\boldsymbol{\psi}} }_{i}{{\boldsymbol{\psi}} }_{i}^{\text{T}}\right)-\frac{{\lambda }_{1}^{2}{\lambda }_{3}^{2}}{2{\lambda }_{\mathrm{m}\mathrm{i}\mathrm{n}}\left({\mathcal{R}}_{i}\right)}\right)\|{\widetilde{{\boldsymbol{W}}}}_{ci}\left({{\boldsymbol{p}}}_{i}\right){\|}^{2}. \end{split} $$ 因此,根据Lyapunov稳定性定理和式(37),当
$$ \left\|{{{\boldsymbol{p}}}}_{{i}}\right\| > \sqrt{\dfrac{{{{\lambda }}_{1}^{2}{{\lambda }}_{5}^{2}}/{{{\lambda }}_{\mathrm{m}\mathrm{i}\mathrm{n}}\left(\mathcal{R}_{i}\right)}+{\gamma }_{ci}{{\lambda }}_{6}^{2}}{2{{\lambda }}_{\mathrm{m}\mathrm{i}\mathrm{n}}\left({{\boldsymbol{Q}}}_{i}\right)}}$$ 或
$ \left\|{\widetilde{{\boldsymbol{W}}}}_{ci}\left({{\boldsymbol{p}}}_{i}\right)\right\| > \sqrt{\dfrac{{{\lambda }}_{1}^{2}{{\lambda }}_{5}^{2}+{{\gamma }}_{ci}{{\lambda }}_{6}^{2}{{\lambda }}_{\min}\left({\mathcal{R}}_{i}\right)}{{{\gamma }}_{ci}{{\lambda }}_{\min}\left({{{\boldsymbol{\psi}} }}_{i}{{{\boldsymbol{\psi}} }}_{i}^{\text{T}}\right){{\lambda }}_{\min}\left({\mathcal{R}}_{i}\right)-{{\lambda }}_{1}^{2}{{\lambda }}_{3}^{2}}}\triangleq {{\lambda }}_{7} $ 其中任意一式成立,独立子系统状态
$ {{p}}_{i} $ 和局部评判神经网络权重估计误差$ {\widetilde{{{W}}}}_{ci}\left({{{p}}}_{i}\right) $ 均为最终一致有界的.证毕.由定理1和式(27)、(31)可得,
$ \|{V}_{i}^{*}\left({{{p}}}_{i}\right)-{\widehat{{V}}}_{i}\left({{{p}}}_{i}\right)\|\leqslant {\lambda }_{2}{\lambda }_{7}+{\lambda }_{4} $ .通过选取恰当的学习率$ {\gamma }_{ci} $ 可以对$ {\lambda }_{7} $ 进行调整.因此,$ {\widehat{{{{V}}}}}_{i}\left({{{{{p}}}}}_{i}\right) $ 能够收敛到子系统最优代价函数$ {V}_{i}^{*}\left({{{p}}}_{i}\right) $ 的邻域内.4 仿真研究
本章将采用2个仿真算例来验证所提出针对状态约束互联非线性系统的分散镇定方法的有效性.
4.1 数值非线性系统
考虑互联非线性系统,其动力学模型为
$$ \begin{split} {\dot{{\boldsymbol{x}}}}_{1}=&\left[\begin{array}{c}-{x}_{11}+{x}_{12}\\ -0.5\left({x}_{11}+{x}_{12}\right)+0.5{x}_{12}{\left(2+\mathrm{cos}\left(2{x}_{11}\right)\right)}^{2}\end{array}\right]+\\ &\left[\begin{array}{c}0\\ 2+\mathrm{cos}\left(2{x}_{11}\right)\end{array}\right]{{\boldsymbol{u}}}_{1}+{{\boldsymbol{z}}}_{1}\left({\boldsymbol{x}}\right),\end{split} $$ (44) $$ \begin{split} {\dot{{\boldsymbol{x}}}}_{2}=&\left[\begin{array}{c}0.5{x}_{22}\\ -{x}_{21}-0.5{x}_{22}+0.5{x}_{21}^{2}{x}_{22}\end{array}\right] +\\ &\left[\begin{array}{c}0\\ {x}_{21}\end{array}\right]{{\boldsymbol{u}}}_{2}+{{\boldsymbol{z}}}_{2}\left({\boldsymbol{x}}\right).\end{split} $$ (45) 2个子系统的耦合项分别设为
$$ {{\boldsymbol{z}}}_{1}\left({\boldsymbol{x}}\right)=\left[\begin{array}{c}0.25\\ 0.25\end{array}\right]\left({x}_{11}+{x}_{22}\right){\mathrm{sin}}^{2}{x}_{22}\mathrm{cos}\;{x}_{21}, $$ $$ {{\boldsymbol{z}}}_{2}\left({\boldsymbol{x}}\right)=\left[\begin{array}{c}0.2\\ 0\end{array}\right]\left({x}_{12}+{x}_{22}\right)\mathrm{cos}\left({{\rm{e}}}^{{x}_{21}^{2}}\right). $$ 在此例中,初始状态分别选择为
$ {{{\boldsymbol{x}}}}_{1}\left(0\right)={\left[\mathrm{1,0}\right]}^{\text{T}} $ ,$ {{\boldsymbol{x}}}_{2}\left(0\right)={\left[1,-1\right]}^{\text{T}} $ .状态约束为$ {x}_{11},{x}_{12}\in \left(-0.2,2\right) $ ,$ {x}_{21}\in (-1.5,1.5) $ ,$ {x}_{22}\in (-1.4,1.5) $ .下面利用坐标变换构造无约束的系统.经过坐标变换后的初始状态为
$ {{\boldsymbol{p}}}_{1}\left(0\right)=[{F}_{b}\left(1;-0.2,2\right), {F}_{b}(0; -0.2,2)]^{\text{T}} $ ,$ {{\boldsymbol{p}}}_{2}\left(0\right)=\left[{F}_{b}\left(1;-1.5,1.5\right),\right.{\left.{F}_{b}\left(-1;-1.4,1.5\right)\right]}^{\text{T}} $ .独立子系统的代价函数中选取$ {{\boldsymbol{Q}}}_{1}={{\boldsymbol{Q}}}_{2}=\text{diag}\left\{6,6\right\} $ ,$ {\mathcal{R}}_{1}={\mathcal{R}}_{2}= \text{diag}\left\{1,0.3\right\} $ .构造2个局部评判神经网络分别估计2个独立子系统镇定律.激活函数选为
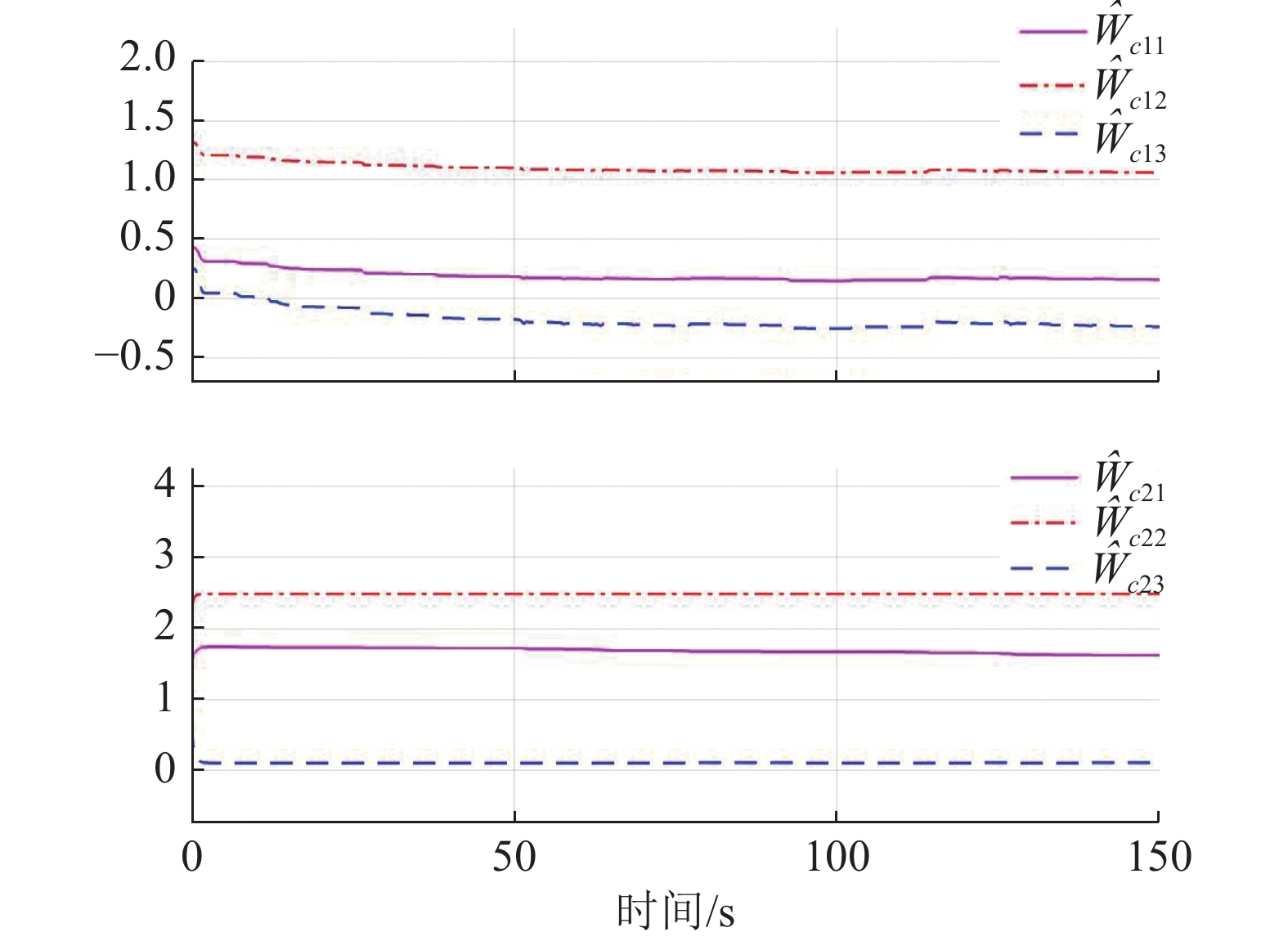
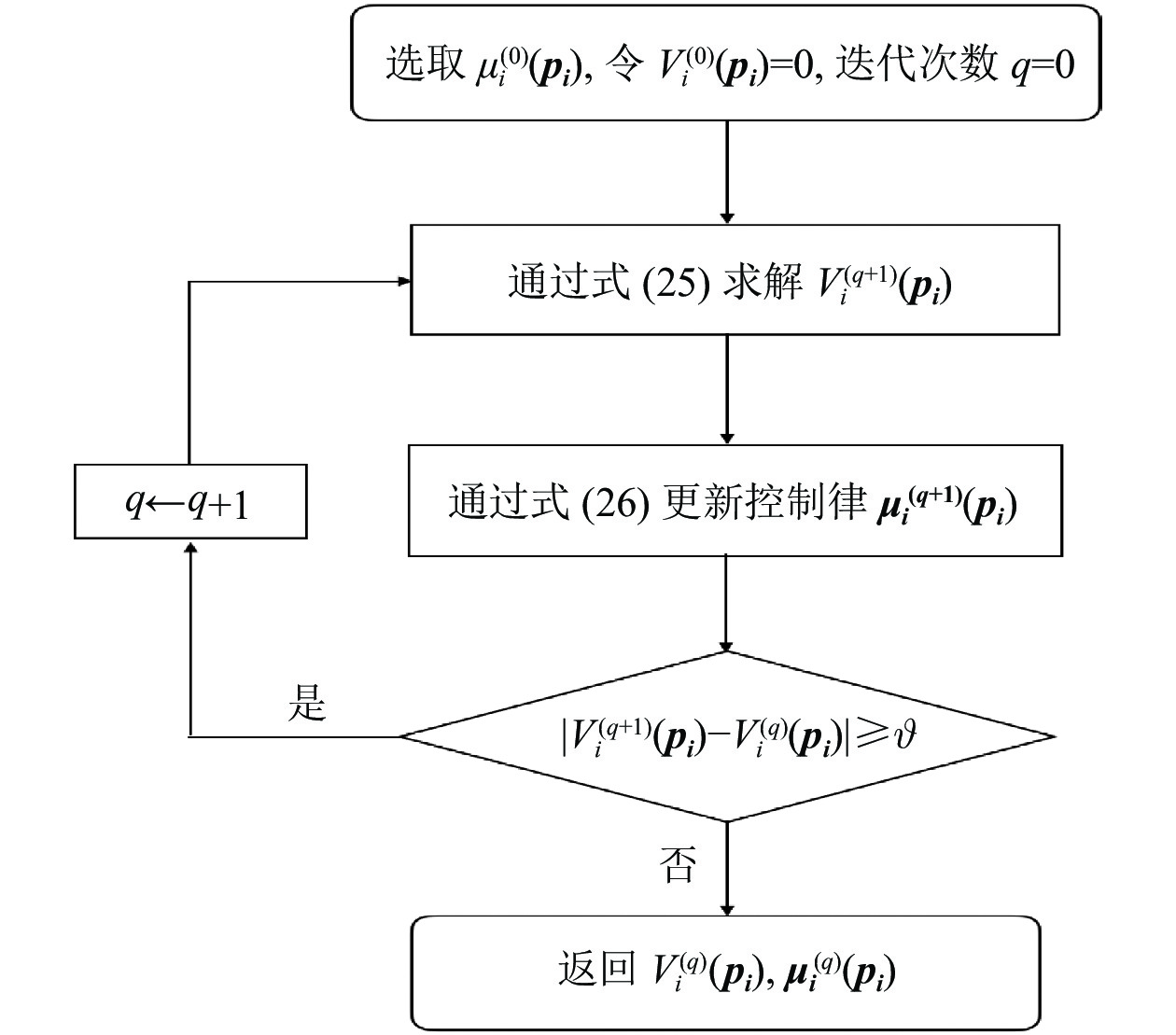
$ {\mathrm{{\boldsymbol{{\boldsymbol{\sigma}}}} }}_{ci}\left({{\boldsymbol{p}}}_{i}\right)={\left[{p}_{i1}^{2},{{{p}}}_{i2}^{2},{p}_{i1}{p}_{i2}\right]}^{\text{T}} $ ,$ i=\mathrm{1,2} $ .根据子系统的初始可容许镇定律,局部评判神经网络初值权重选取为$ {\widehat{{\boldsymbol{W}}}}_{c1}^{\left(0\right)}={\left[\mathrm{0,1},0\right]}^{\text{T}} $ ,$ {\widehat{{\boldsymbol{W}}}}_{c2}^{\left(0\right)}={\left[\mathrm{1,2},1\right]}^{\text{T}} $ ,学习率选取为$ {\mathrm{\gamma }}_{c1}={\mathrm{\gamma }}_{c2}=0.1 $ .如图2所示,采用式(35)作为更新律训练2个独立子系统的局部评判神经网络150 s后,2个独立子系统的局部评判神经网络权重分别收敛于
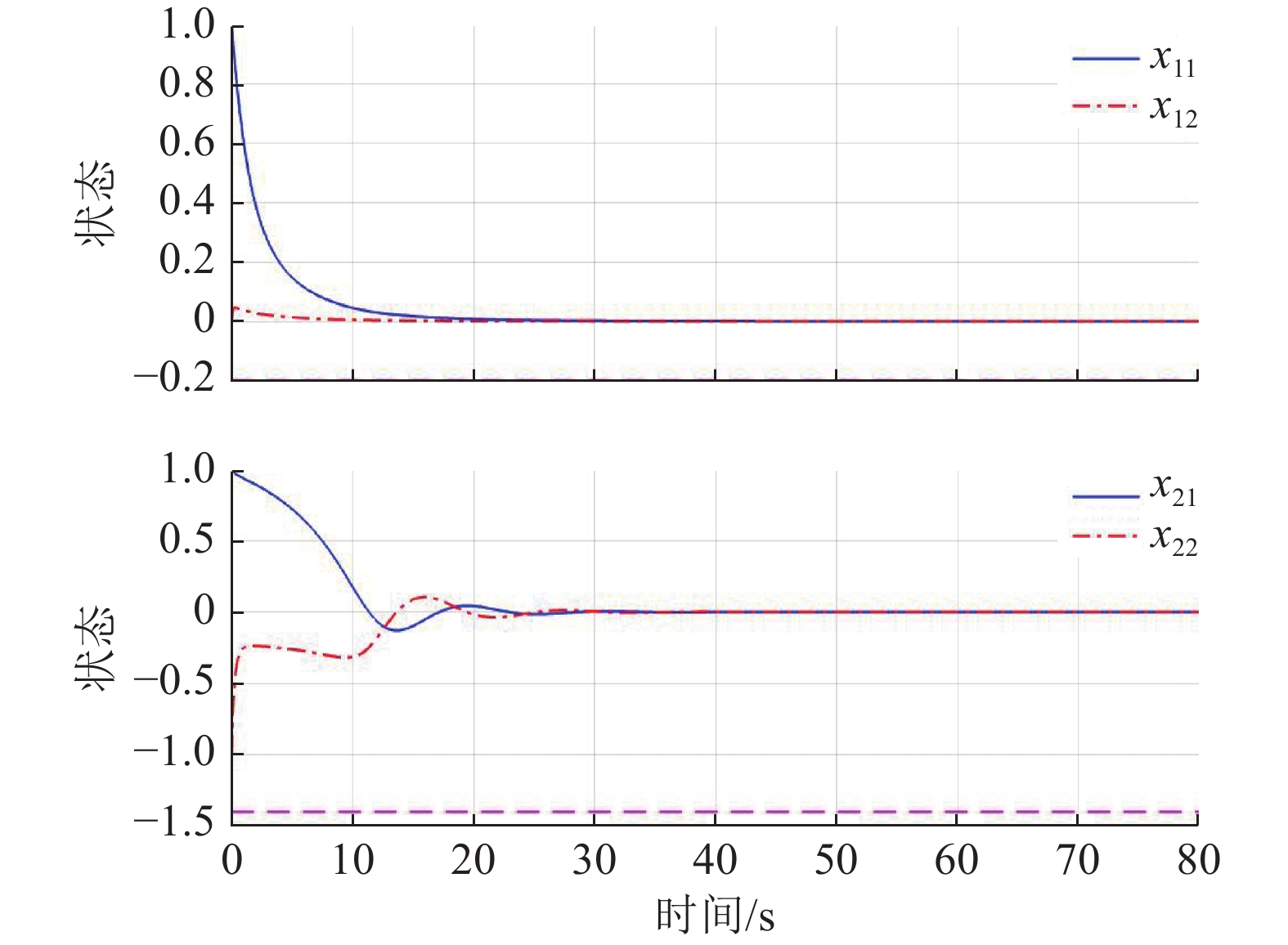
$$ \begin{split}&{\widehat{{\boldsymbol{W}}}}_{c1}={\left[0.157\;4,1.059\;5,-0.239\;0\right]}^{\text{T}},\\ &{\widehat{{\boldsymbol{W}}}}_{c2}={\left[1.623\;4,2.486\;4,0.110\;8\right]}^{\text{T}}. \end{split}$$ 图3所示为分散镇定方法的作用下,原互联子系统(44)、(45)的状态演化过程.由此可见,原系统的2个互联子系统状态能够收敛到平衡点附近的小邻域内,即最终一致有界,且满足状态约束.
为了验证系统状态约束对系统镇定性能的影响,在不处理状态约束的情况下,直接采用了现有基于ADP的分散镇定方法对系统(44)、(45)进行控制,得到的系统状态演化过程如图4所示.由仿真结果可见,虽然该方法能获得更快的收敛速度,但系统状态超出了约束区间.
4.2 双倒立摆系统
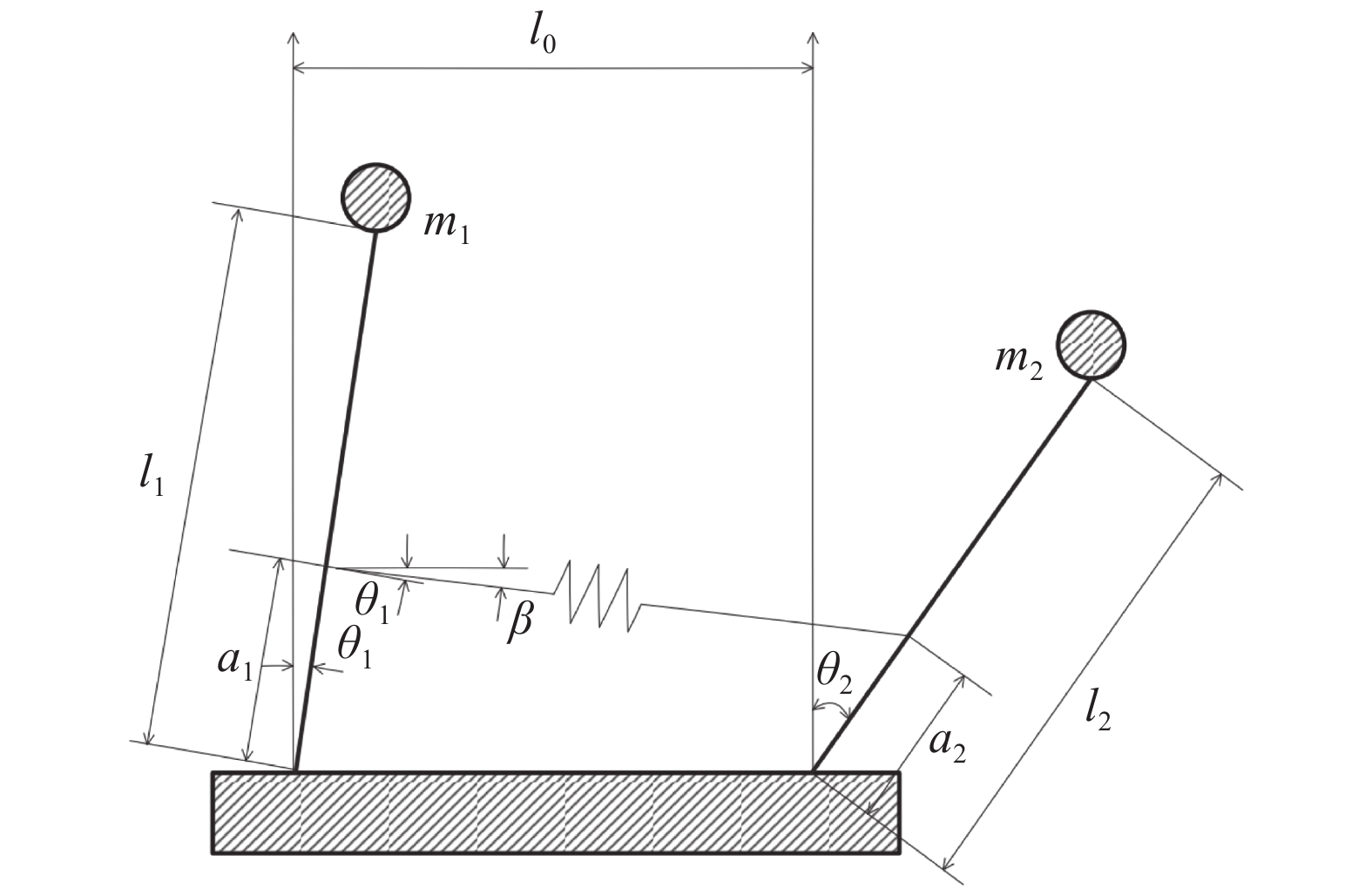
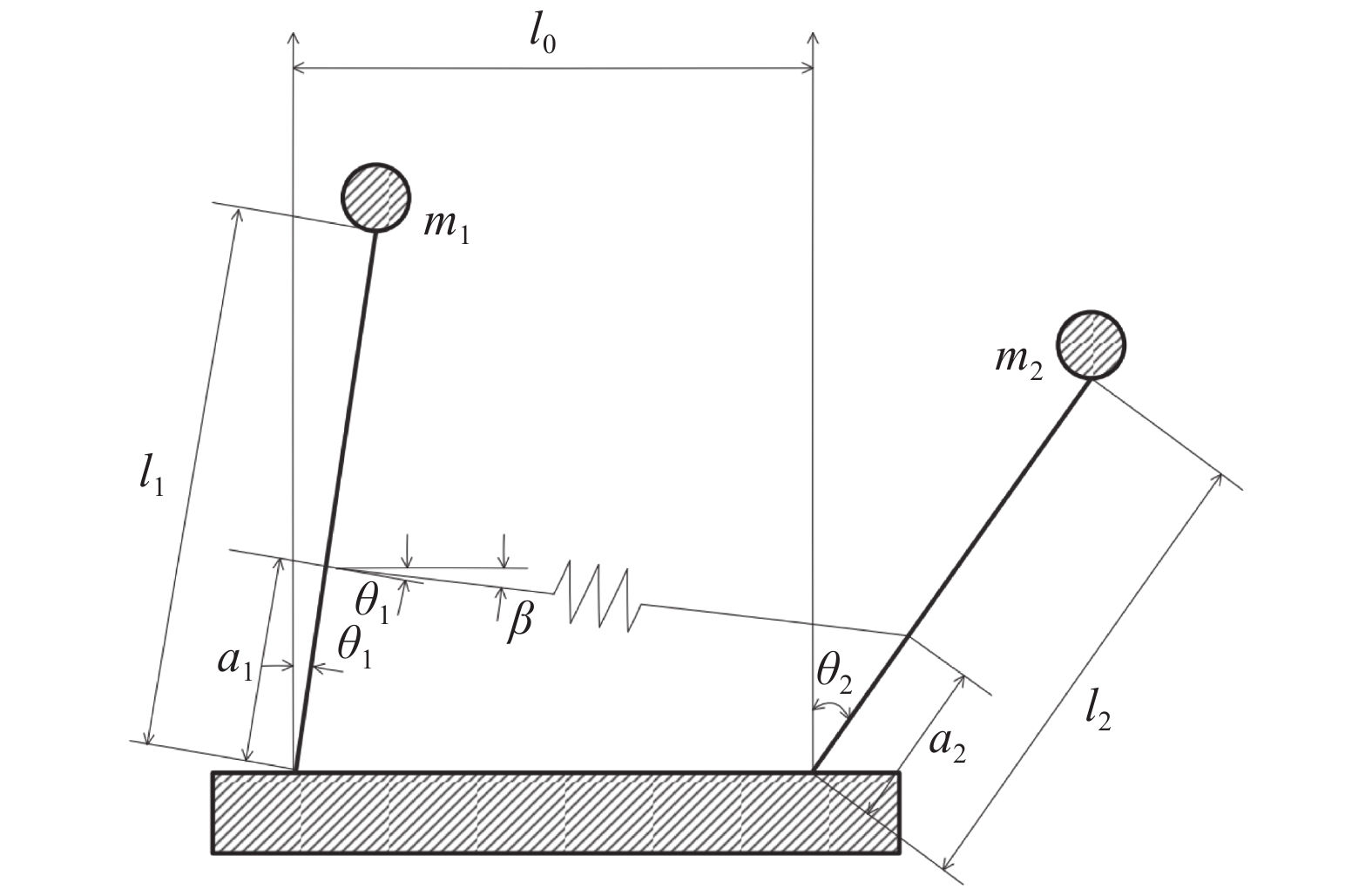
采用双倒立摆系统进行仿真[22],以进一步验证本文所提方法的有效性.由弹簧连接的双倒立摆系统如图5所示,可看作含2个子系统的互联非线性系统,动力学模型可表示为
$$ \begin{split} &{m}_{1}{l}_{1}^{2}\ddot{{\theta }_{1}}-{m}_{1}g{l}_{1}\mathrm{sin}\;{\theta }_{1}+{b}_{1}{\dot{\theta }}_{1}-F{a}_{1}\mathrm{cos}\left({\theta }_{1}-\beta \right)={\delta }_{1}{{u}}_{1},\\ &{m}_{2}{l}_{2}^{2}\ddot{{\theta }_{2}}-{m}_{2}g{l}_{2}\mathrm{sin}\;{\theta }_{2}+{b}_{2}{\dot{\theta }}_{2}-F{a}_{2}\mathrm{cos}\left({\theta }_{2}-\beta \right)={\delta }_{2}{{u}}_{2}. \end{split} $$ 式中,
$ {b}_{1} $ 和$ {b}_{2} $ 分别为2个弹簧的阻尼系数,$$ \begin{array}{c} F=k\{1+ {A}^{2}{({l}_{k}-{l}_{0})}^{2}\}({l}_{k}-{l}_{0}) , \\ \left|A\left({l}_{k}-{l}_{0}\right)\right| < 1 , \\{\beta }={\text{arctan}} \dfrac{{a}_{1}\mathrm{cos}\;{\theta }_{1}-{a}_{2}\mathrm{cos}\;{\theta }_{2}}{{l}_{0}-{a}_{1}\mathrm{sin}\;{\theta }_{1}+{a}_{2}\mathrm{sin}\;{\theta }_{2}} ,\\ {l}_{k}={\left\{{\left({l}_{0}-{a}_{1}\mathrm{sin}\;{\mathrm{\theta }}_{1}+{a}_{2}\mathrm{sin}\;{\mathrm{\theta }}_{2}\right)}^{2}+{\left({a}_{1}\mathrm{cos}\;{\mathrm{\theta }}_{1}+{a}_{2}\mathrm{cos}\;{\mathrm{\theta }}_{2}\right)}^{2}\right\}}^{2}. \end{array}$$ 系统参数选取为
$ {\mathrm{\delta }}_{1}={\mathrm{\delta }}_{2}=1 $ ,$ {m}_{1}={m}_{2}=1\;{\rm{kg}} $ ,$ {l}_{1}={l}_{2}= 0.5\;{\rm{m}} $ ,$ {l}_{0}=1\;{\rm{m}} $ ,$ g=9.8\;{\rm{m\cdot s^{-2}}} $ ,$ {b}_{1}={b}_{2}=0.009 $ ,$ k=30 $ ,$ A=0.1 $ ,弹簧与2个倒立摆底端的距离$ {a}_{1}={a}_{2}=0.1 $ .状态约束为$ {\dot{\theta }}_{1}\in \left(-\mathrm{1,1}\right) $ ,$ {\dot{\theta }}_{2}\in \left(-\mathrm{1.3,1.3}\right) $ .令
$ {x}_{i1}={\theta }_{i} $ ,$ {x}_{i2}={\dot{\theta }}_{i} $ ,系统状态的初始值为$ {x}_{1}\left(0\right)= {\left[-\mathrm{2,0.3}\right]}^{\text{T}} $ ,$ {x}_{2}\left(0\right)={\left[\mathrm{1,0}\right]}^{\text{T}} $ ,其中$ i=1,2 $ .2个互联子系统的动力学模型为$$ {{\boldsymbol{f}}}_{i}\left({{\boldsymbol{x}}}_{i}\right)=\left[\begin{array}{c}{x}_{i2}\\ 5.88\mathrm{sin}\;{x}_{i1}-0.036{x}_{i2}\end{array}\right], $$ $$ {{\boldsymbol{g}}}_{i}\left({{\boldsymbol{x}}}_{i}\right)=\left[\begin{array}{c}0\\ {\delta }_{i}\end{array}\right], {{\boldsymbol{k}}}_{i}\left({\boldsymbol{x}}\right)=\left[\begin{array}{c}0\\ 4F{a}_{i}\mathrm{cos}\left({x}_{i1}-\beta \right)\end{array}\right]. $$ 对原系统进行坐标变换并构造独立子系统,选取代价函数中的参数为
$ {{\boldsymbol{Q}}}_{1}=\text{diag}\left\{\mathrm{0.1,0.1}\right\} $ ,$ {{\boldsymbol{Q}}}_{2}=\text{diag} \left\{0.2,\right. \left.0.2\right\} $ ,$ {\cal{{\boldsymbol{R}}}}_{1}=\text{diag}\left\{\mathrm{0.01,0.002\;5}\right\} $ ,$ {\mathcal{{\boldsymbol{R}}}}_{2}=\text{diag}\left\{\mathrm{0.02,0.002\;5}\right\} $ .构造2个局部评判神经网络分别估计两个独立子系统镇定律.激活函数选为
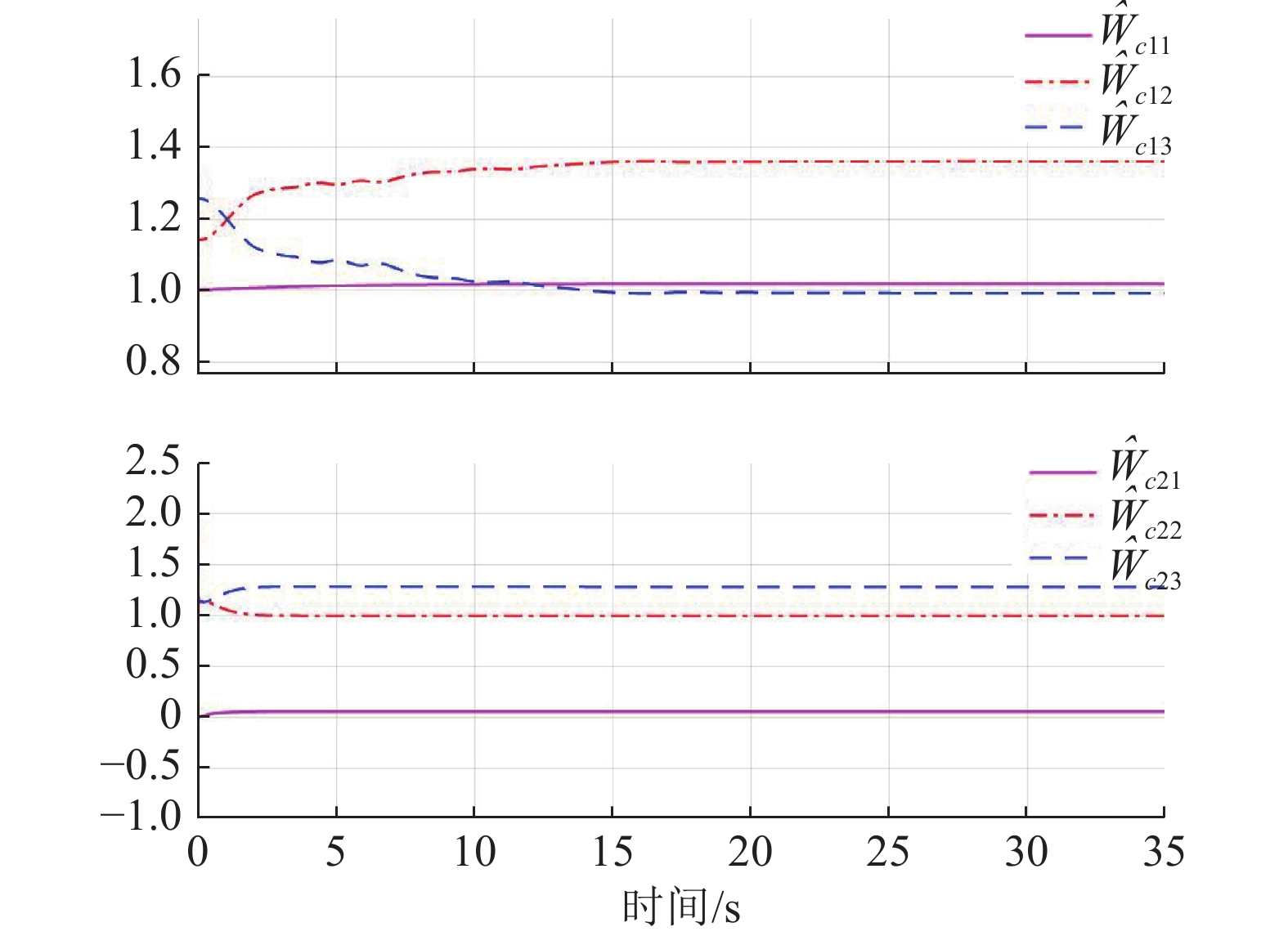
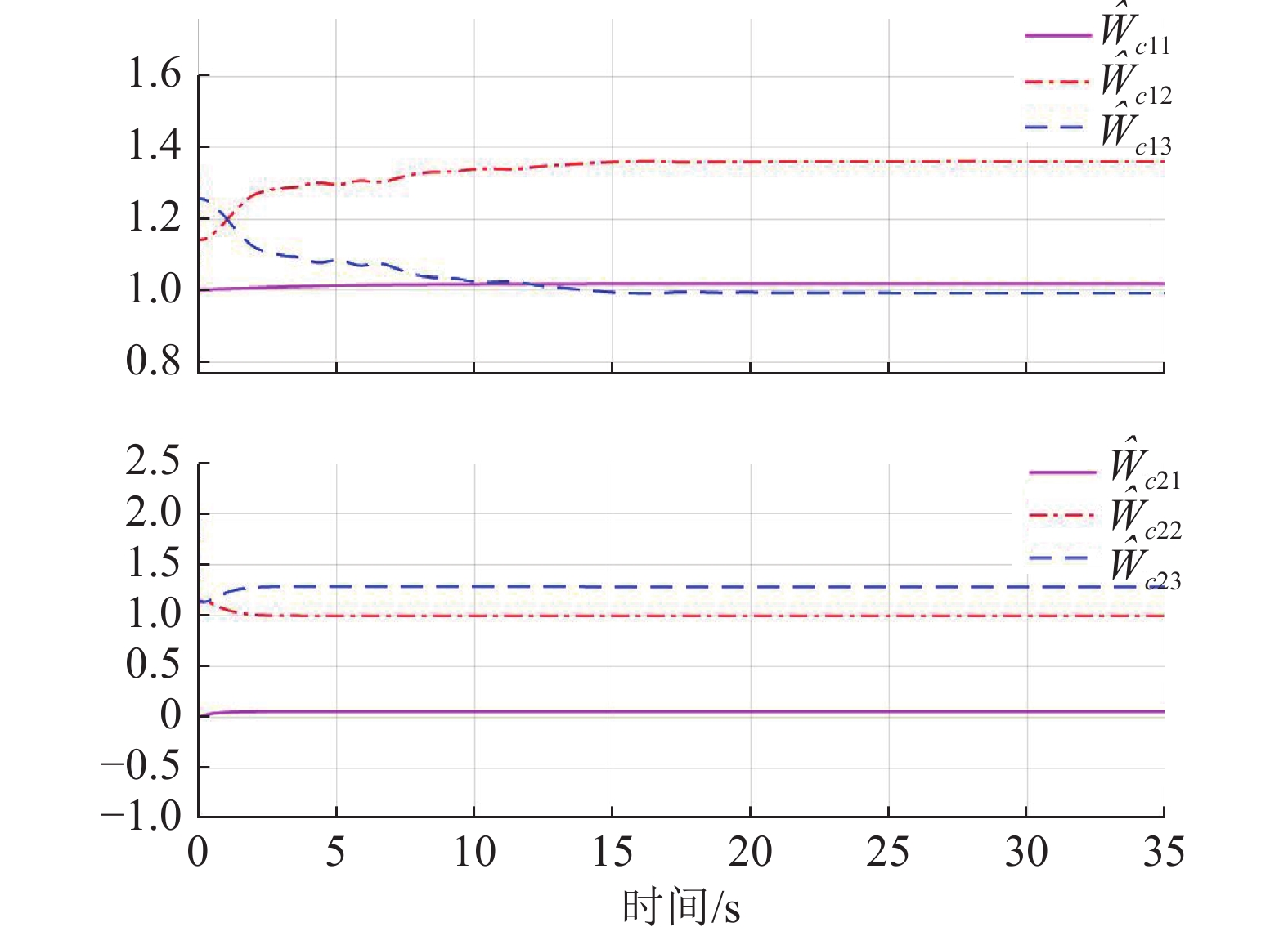
$ {{\boldsymbol{{\boldsymbol{\sigma}}}} }_{ci}\left({{{{\boldsymbol{p}}}}}_{i}\right)={\left[{{{p}}}_{i1}^{2},{p}_{i2}^{2},{p}_{i1}{p}_{i2}\right]}^{\text{T}} $ ,$ i=\mathrm{1,2} $ .根据子系统的初始可容许镇定律,局部评判神经网络权重初值选取为$ {\widehat{{\boldsymbol{W}}}}_{c1}^{\left(0\right)}={\left[\mathrm{1,1.5,1}\right]}^{\text{T}} $ 和$ {\widehat{{\boldsymbol{W}}}}_{c2}^{\left(0\right)}= {\left[\mathrm{0,1},2\right]}^{\text{T}} $ ,学习率选取为$ {\mathrm{\gamma }}_{c1}={\mathrm{\gamma }}_{c2}=0.1 $ .图6所示为2个独立子系统的局部评判神经网络权重演化过程,可见其分别收敛到
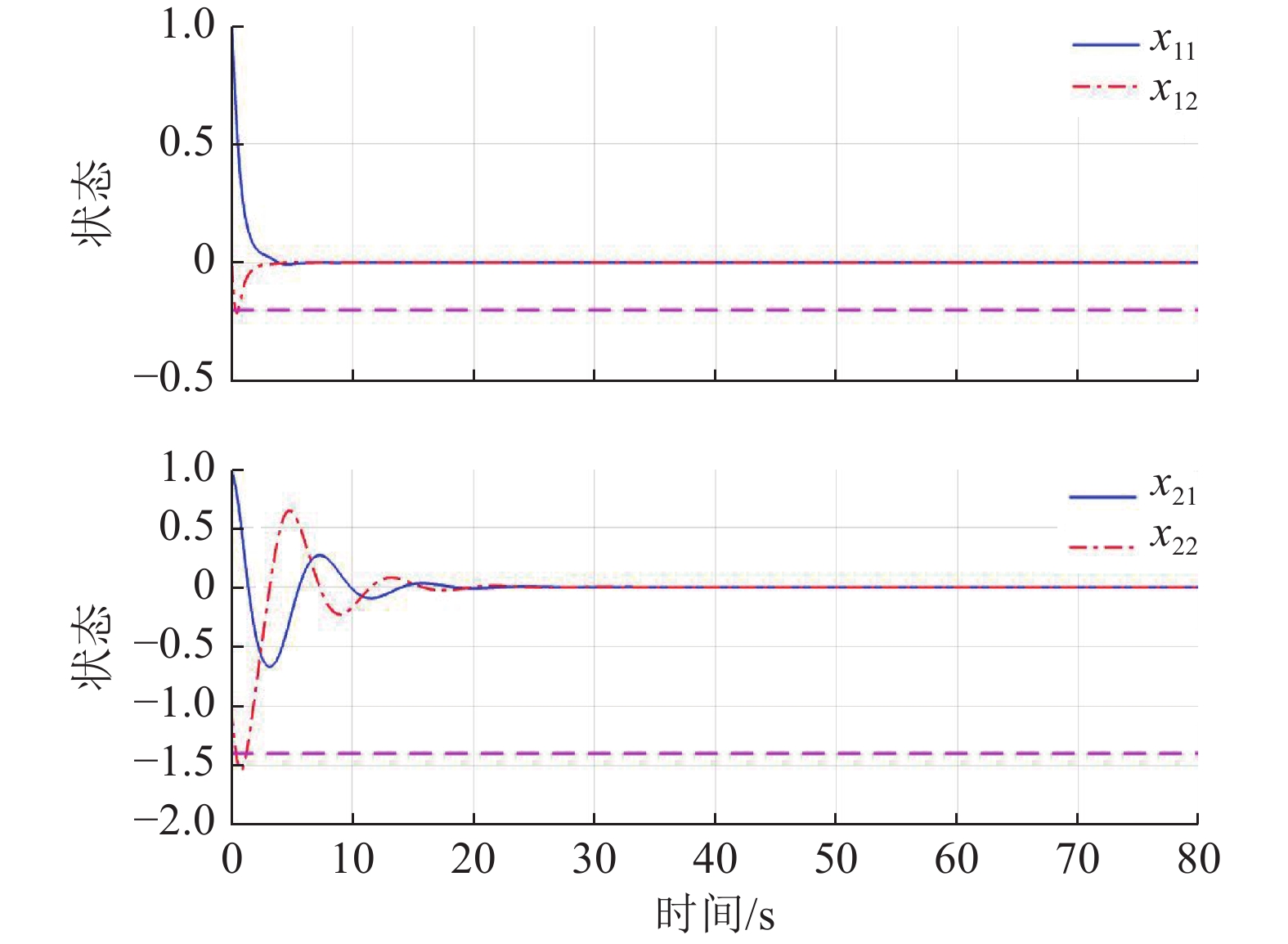
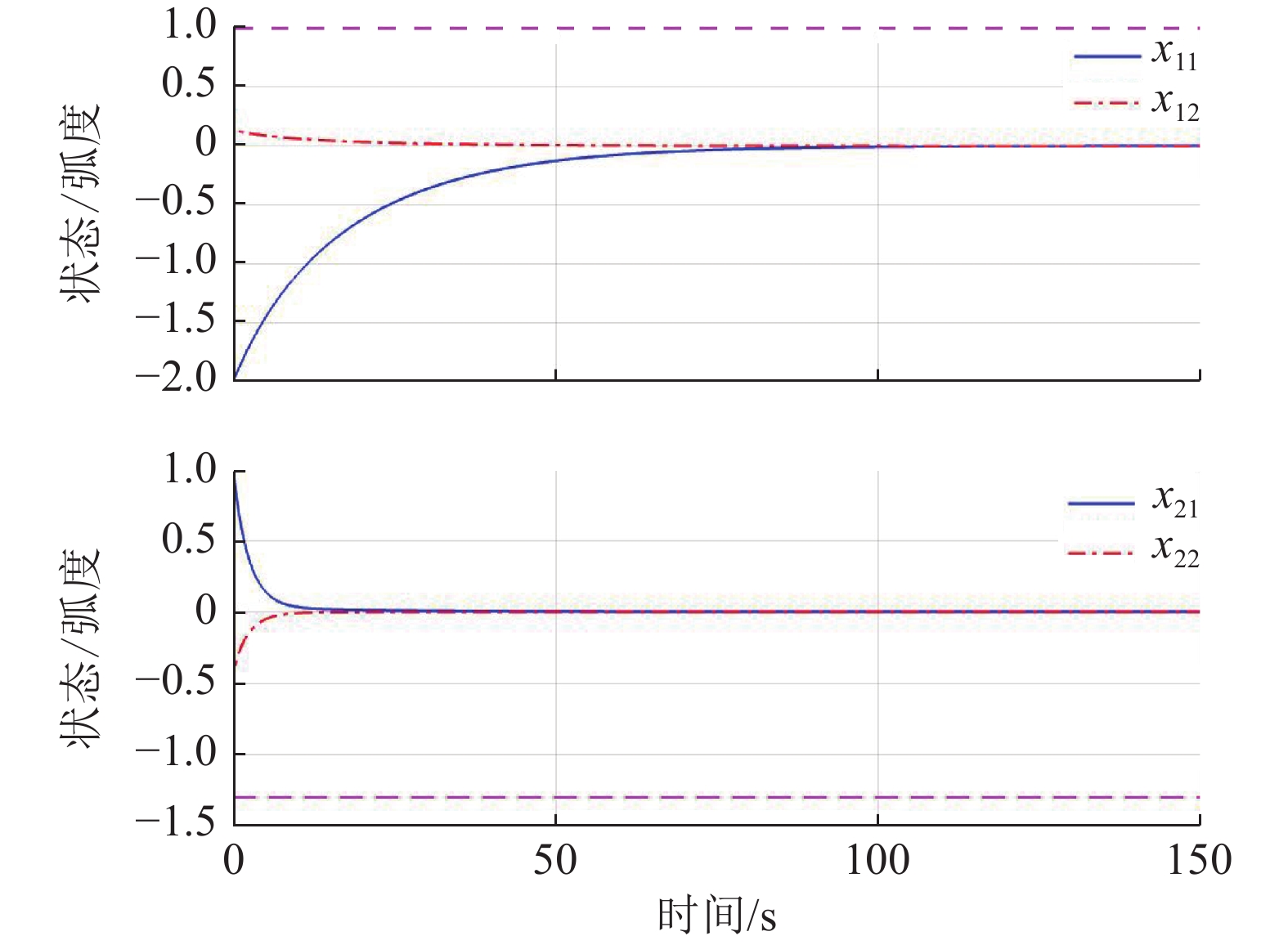
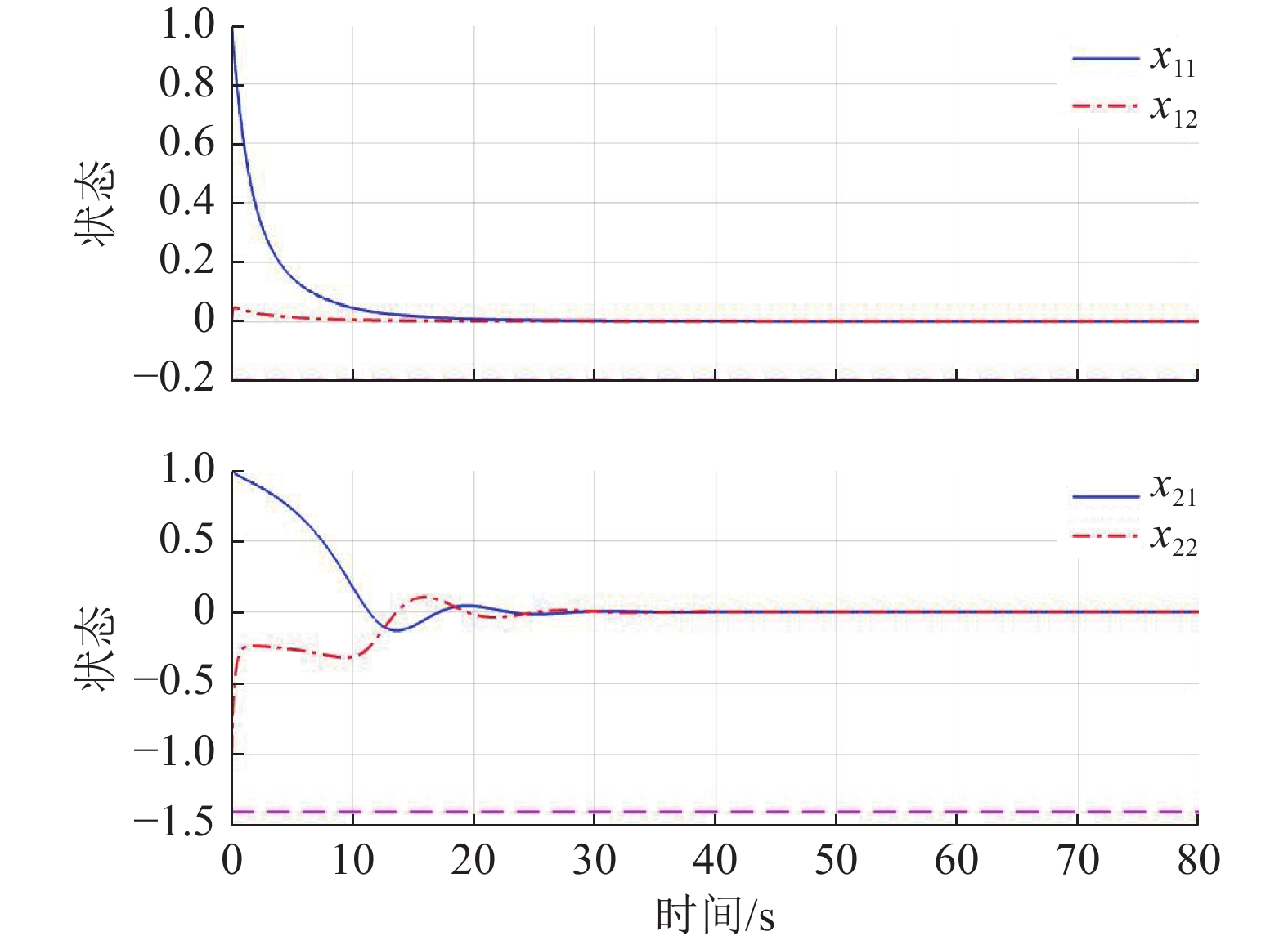
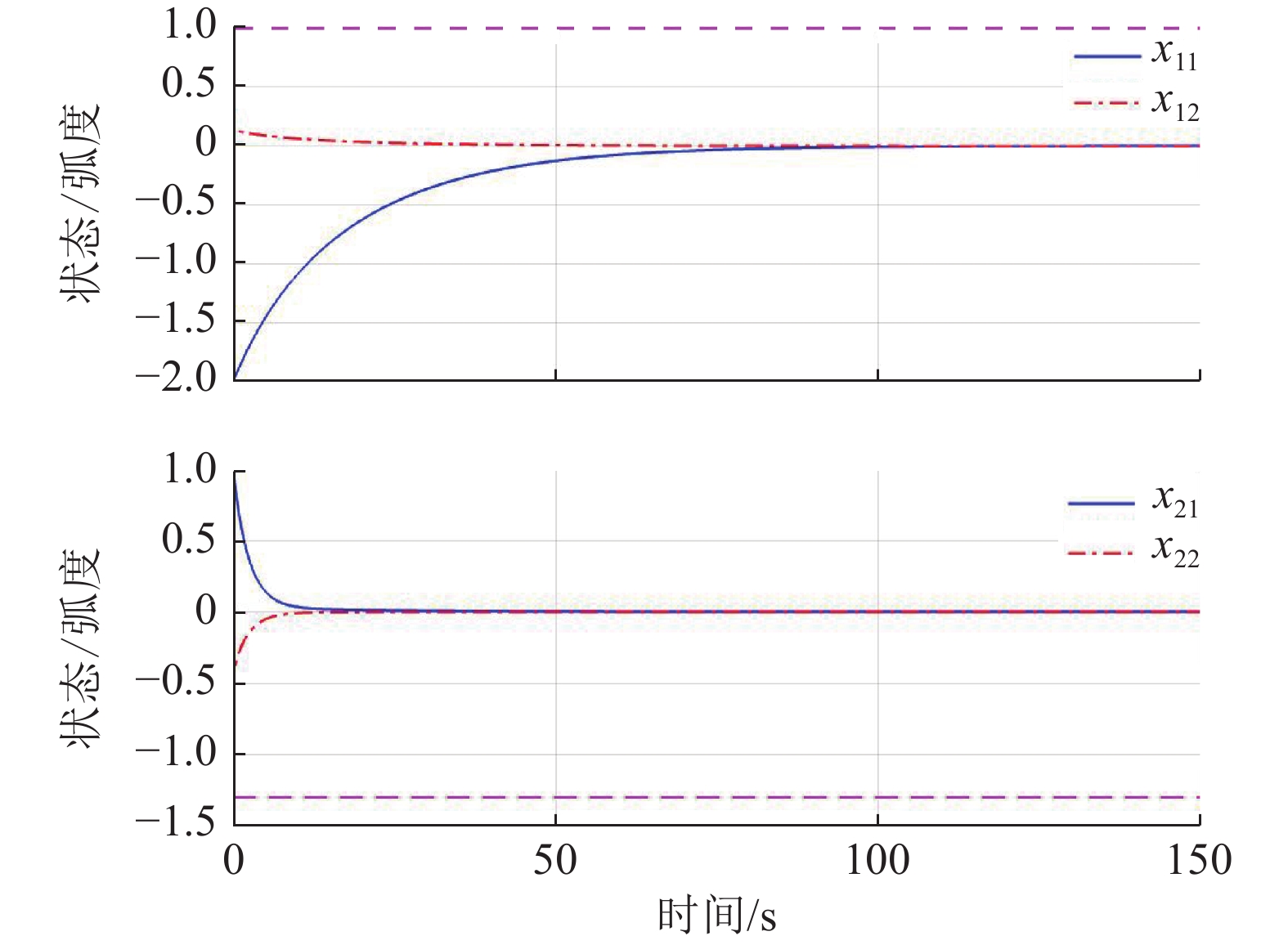
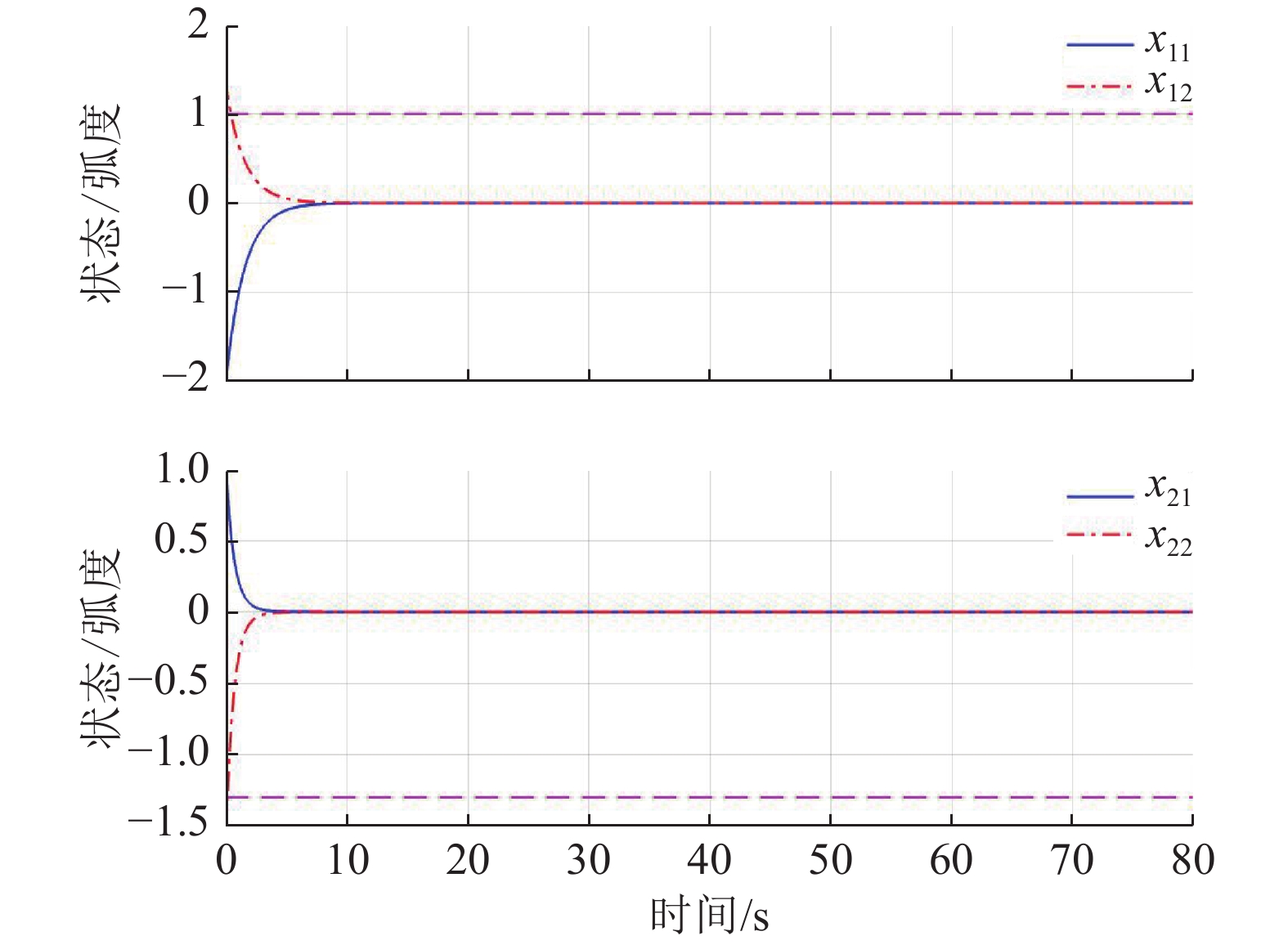
$$\begin{split} &{\widehat{{\boldsymbol{W}}}}_{c1}={\left[1.017\;9,1.360\;2,0.992\;6\right]}^{\text{T}},\\ &{\widehat{{\boldsymbol{W}}}}_{c2}={\left[0.053\;1,0.989\;1,1.275\;3\right]}^{\text{T}}. \end{split}$$ 图7所示为双倒立摆系统在本文所提的分散镇定方法作用下的状态演化过程.由于倒立摆位置和角速度的初值不处于平衡状态,因此在施加控制后的0~1 s内系统状态x12和x22有短暂的调节过程,但系统状态始终未超出状态约束,并达到最终一致有界.
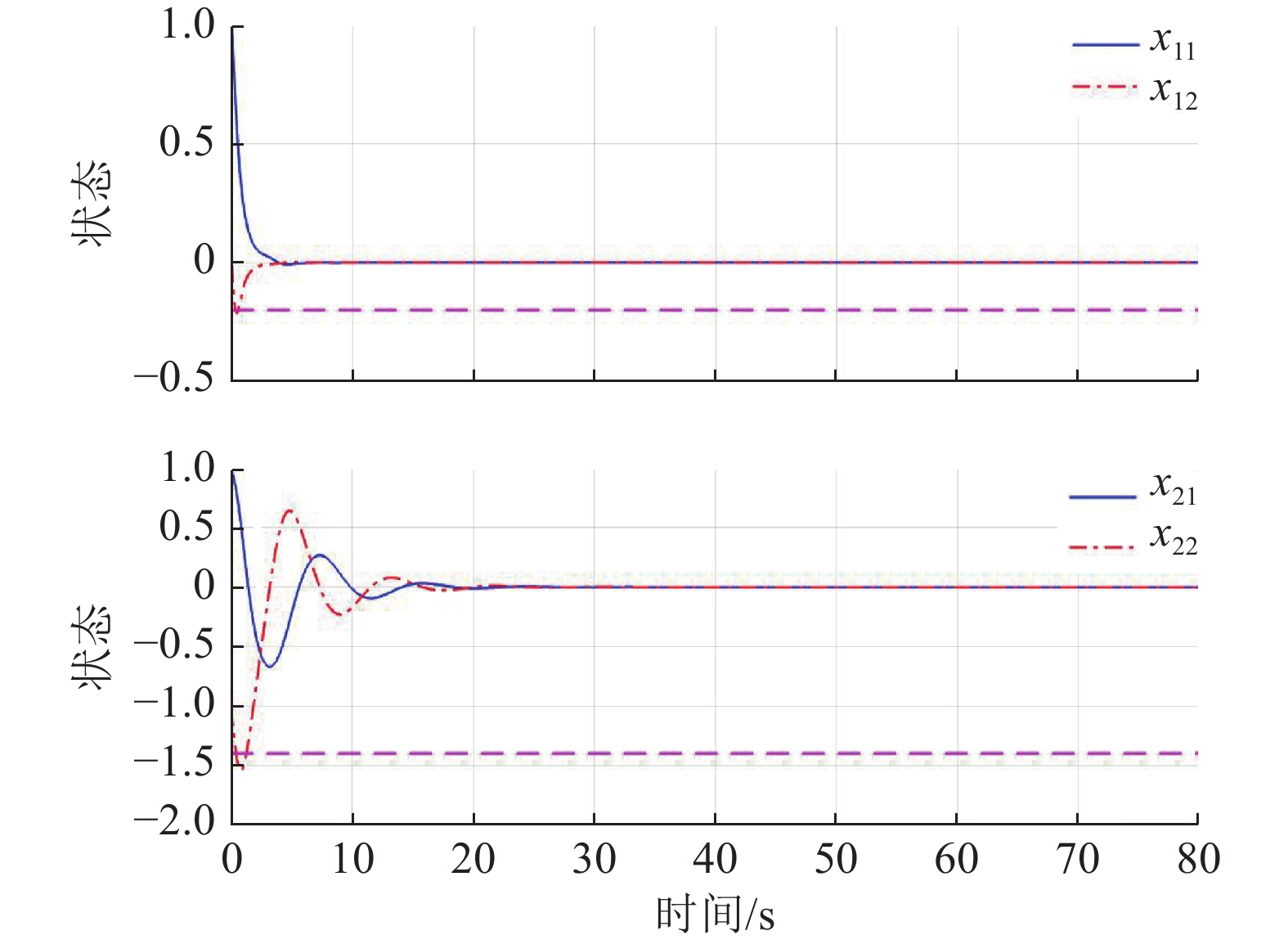
作为对比,本例也采用了未考虑状态约束的基于ADP的分散镇定方法进行仿真,结果如图8所示.在该方法作用下,系统所用的调节时间与图7相比较短,
$ {x}_{12} $ 和$ {x}_{22} $ 在超出状态约束之后再收敛.因此,本文所提方法通过更长的调节时间换取了系统性能的保证.5 结论
本文针对一类含有常值型状态约束的互联非线性系统,提出了一种基于ADP的分散镇定方法.该方法首先引入边界函数进行坐标变换,将含状态约束系统的镇定问题转化为无约束系统的镇定问题,进而构造独立子系统,并引入辅助控制构成增广镇定律,以补偿耦合项的影响.通过局部评判神经网络对各个独立子系统的增广镇定律进行近似求解,并利用Lyapunov稳定性定理证明了系统状态与局部评判神经网络的权重估计误差均为最终一致有界的.仿真结果表明,所提出的分散镇定方法是有效的.
-
[1] 夏宏兵. 非线性系统的自学习优化安全调控方法研究[D]. 北京:北京师范大学,2023 [2] BIAN T,JIANG Y,JIANG Z P. Decentralized adaptive optimal control of large-scale systems with application to power systems[J]. IEEE Transactions on Industrial Electronics,2015,62(4):2439 doi: 10.1109/TIE.2014.2345343
[3] EL-ATTAR R,VIDYASAGAR M. Subsystem simplification in large-scale systems analysis[J]. IEEE Transactions on Automatic Control,1979,24(2):321 doi: 10.1109/TAC.1979.1102004
[4] YANG X,HE H B. Adaptive dynamic programming for decentralized stabilization of uncertain nonlinear large-scale systems with mismatched interconnections[J]. IEEE Transactions on Systems,Man,and Cybernetics:Systems,2020,50(8):2870
[5] WANG D,HE H B,LIU D R. Adaptive critic nonlinear robust control:a survey[J]. IEEE Transactions on Cybernetics,2017,47(10):3429 doi: 10.1109/TCYB.2017.2712188
[6] ZHAO B,SHI G,LIU D R. Event-triggered local control for nonlinear interconnected systems through particle swarm optimization-based adaptive dynamic programming[J/OL]. IEEE Transactions on Systems,Man,and Cybernetics:Systems, http://dx.doi.org/10.1109/TSMC.2023.3298065
[7] ZHAO B,ZHANG Y W,LIU D R. Adaptive dynamic programming-based cooperative motion/force control for modular reconfigurable manipulators:a joint task assignment approach[J/OL]. IEEE Transactions on Neural Networks and Learning Systems, http://dx.doi.org/10.1109/TNNLS.2022.3171828
[8] LEWIS F L,VRABIE D. Reinforcement learning and adaptive dynamic programming for feedback control[J]. IEEE Circuits and Systems Magazine,2009,9(3):32 doi: 10.1109/MCAS.2009.933854
[9] LEWIS F L,VRABIE D,VAMVOUDAKIS K G. Reinforcement learning and feedback control:using natural decision methods to design optimal adaptive controllers[J]. IEEE Control Systems Magazine,2012,32(6):76 doi: 10.1109/MCS.2012.2214134
[10] WANG D. Robust policy learning control of nonlinear plants with case studies for a power system application[J]. IEEE Transactions on Industrial Informatics,2020,16(3):1733 doi: 10.1109/TII.2019.2925632
[11] KHIABANI A G,HEYDARI A. Optimal torque control of permanent magnet synchronous motors using adaptive dynamic programming[J]. IET Power Electronics,2020,13(12):2442 doi: 10.1049/iet-pel.2019.1339
[12] LIU R M,LI S K,YANG L X,et al. Energy-efficient subway train scheduling design with time-dependent demand based on an approximate dynamic programming approach[J]. IEEE Transactions on Systems,Man,and Cybernetics:Systems,2020,50(7):2475
[13] ZHAO B,LIU D R,LUO C M. Reinforcement learning-based optimal stabilization for unknown nonlinear systems subject to inputs with uncertain constraints[J]. IEEE Transactions on Neural Networks and Learning Systems,2020,31(10):4330 doi: 10.1109/TNNLS.2019.2954983
[14] LIU Y J,TONG S C,LI D J,et al. Fuzzy adaptive control with state observer for a class of nonlinear discrete-time systems with input constraint[J]. IEEE Transactions on Fuzzy Systems,2016,24(5):1147 doi: 10.1109/TFUZZ.2015.2505088
[15] ZHANG L G,LIU X J. The synchronization between two discrete-time chaotic systems using active robust model predictive control[J]. Nonlinear Dynamics,2013,74(4):905 doi: 10.1007/s11071-013-1009-2
[16] TEE K P,GE S S,TAY E H. Barrier Lyapunov Functions for the control of output-constrained nonlinear systems[J]. Automatica,2009,45(4):918 doi: 10.1016/j.automatica.2008.11.017
[17] FAN Q Y,YANG G H. Nearly optimal sliding mode fault-tolerant control for affine nonlinear systems with state constraints[J]. Neurocomputing,2016,216:78 doi: 10.1016/j.neucom.2016.06.063
[18] XIE C H,YANG G H. Model-free fault-tolerant control approach for uncertain state-constrained linear systems with actuator faults[J]. International Journal of Adaptive Control and Signal Processing,2017,31(2):223 doi: 10.1002/acs.2695
[19] YANG Y L,DING D W,XIONG H Y,et al. Online barrier-actor-critic learning for H∞ control with full-state constraints and input saturation[J]. Journal of the Franklin Institute,2020,357(6):3316 doi: 10.1016/j.jfranklin.2019.12.017
[20] SONG R Z,LIU L,XIA L N,et al. Online optimal event-triggered H∞ control for nonlinear systems with constrained state and input[J]. IEEE Transactions on Systems,Man,and Cybernetics:Systems,2023,53(1):131
[21] VAMVOUDAKIS K G,LEWIS F L. Online actor-critic algorithm to solve the continuous-time infinite horizon optimal control problem[J]. Automatica,2010,46(5):878 doi: 10.1016/j.automatica.2010.02.018
[22] ZHAO B,WANG D,SHI G A,et al. Decentralized control for large-scale nonlinear systems with unknown mismatched interconnections via policy iteration[J]. IEEE Transactions on Systems,Man,and Cybernetics:Systems,2018,48(10):1725




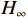
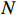
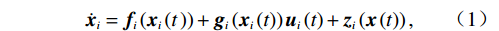
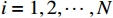
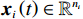
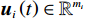
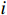
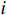
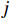
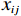
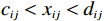
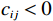
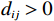
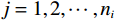
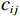
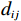
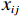
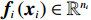
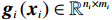
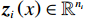
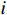
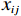
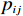
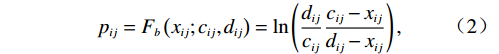
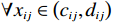
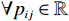
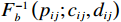
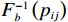
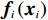
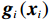
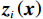
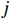
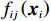
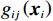
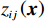
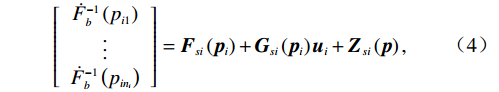
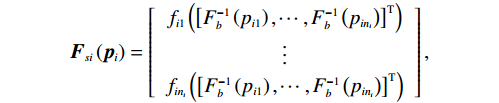
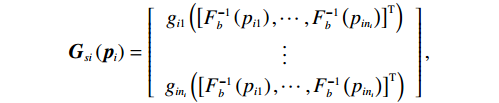
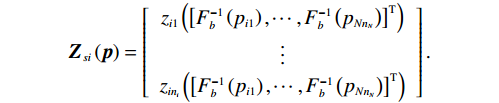
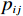
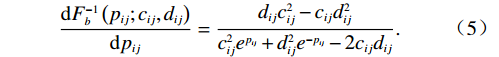
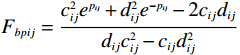
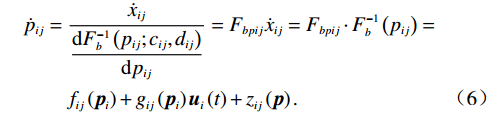
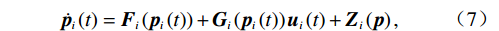
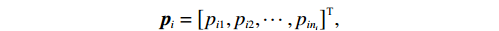
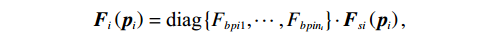
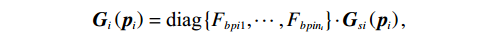
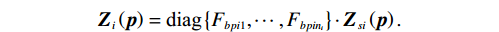
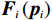
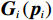
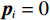
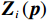
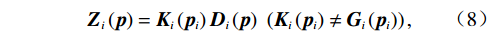
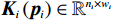
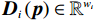
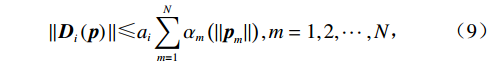
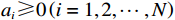
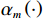
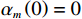
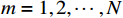
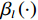
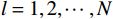
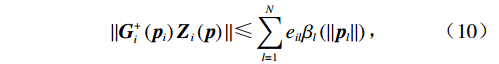
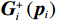
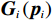
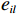
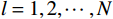
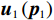
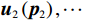
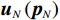
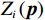
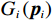
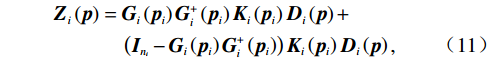
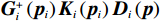
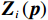

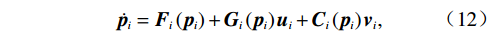
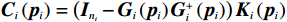
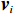
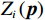
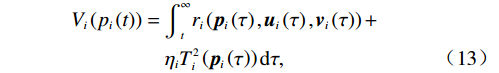
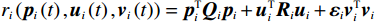
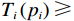
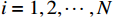
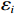
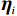
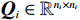

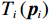
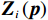
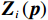
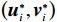
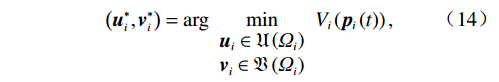
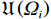
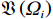
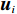
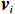
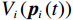
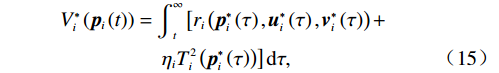
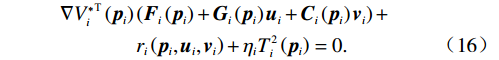
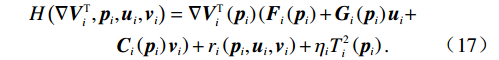
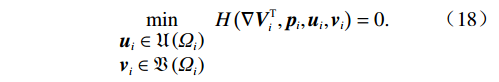
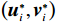
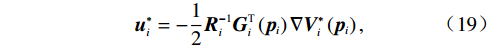
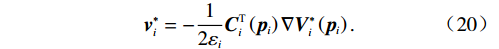
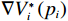
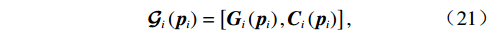
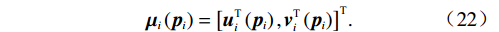
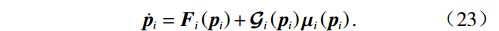
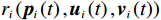
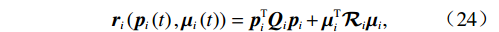
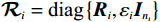
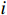
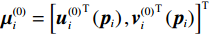
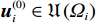
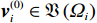
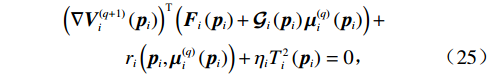
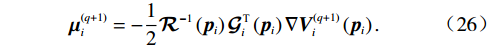
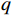
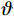
 下载:
下载: